 |
RFOF - RF Library for Orbit Following Codes
|
 |
RFOF - RF Library for Orbit Following Codes
|
Contains exact results for the solution of the stochastic differential equation
![\[ dx(t)=2Cdt+2\sqrt(Cx(t))dw(t) \]](form_118.png)
where 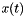 is proportional to the magnetic momentum, the constant
is proportional to the magnetic momentum, the constant 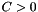 is related to the linear approximation of the diffusion coeeficient !coefficient
is related to the linear approximation of the diffusion coeeficient !coefficient 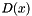 by the local approximation near
by the local approximation near 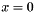 by
by
![\[D(x)=2Cx+O(x^2)\]](form_121.png)
The solution of this SDE is the square of the Bessel process of order 0 and can be represented as
![\[ x(t)=(w_1(Ct)+\sqrt(x_0))^2+(w_2(Ct))^2 \]](form_122.png)
where
![\[ w_1(t), \dots w_2(t)\]](form_123.png)
are independent standard Wiener processes and
![\[x_0=x(t=0)\]](form_124.png)
. More...
Public Member Functions | |
| subroutine | Bessel0 (x_in, delta_t, C_dif, x_fin) |
| Subroutine Bessel0. | |
| subroutine | exact_moments (x_in, delta_t, C_dif, moments) |
| For test of the subroutine Bessel0 only, returns the exact values of the moments of Bessel process Starting point +x_in, duration delta_t, coefficient C_dif The tested subroutine is Bessel0 from module BesselProcess, same notations. | |
| subroutine | Bessel0 (x_in, delta_t, C_dif, x_fin) |
| Subroutine Bessel0 Integration near x=0. | |
| subroutine | Bessel0_General (x_in, delta_t, C_dif, D_0, x_fin) |
| Integration, with local approximation of the diffusion coefficient
| |
| subroutine | exact_moments (x_in, delta_t, C_dif, moments) |
| For test of the subroutine Bessel0 only, returns the exact values of the moments of Bessel process Starting point +x_in, duration delta_t, coefficient C_dif The tested subroutine is Bessel0 from module BesselProcess, same notations. | |
| subroutine | exact_momentsG (x_in, delta_t, C_dif, D_0, moments) |
| For test of the subroutine Bessel0_General only, returns the exact values of the moments of Bessel process Starting point +x_in, duration delta_t, coefficient C_dif, D_0 The tested subroutine is Bessel0_General from module BesselProcess, same notations. | |
| subroutine | Bessel0 (x_in, delta_t, C_dif, x_fin) |
| Integration near x=0, when
| |
| subroutine | Bessel0_General (x_in, delta_t, C_dif, D_0, x_fin) |
| Integration, with local approximation of the diffusion coefficient
The updates are performed according to exact solution of the squared Bessel process of order 0 INPUT: | |
| subroutine | exact_moments (x_in, delta_t, C_dif, moments) |
| For test of the subroutine Bessel0 only, returns the exact values of the moments of Bessel process Starting point +x_in, duration delta_t, coefficient C_dif The tested subroutine is Bessel0 from module BesselProcess, same notations INPUT: | |
| subroutine | exact_momentsG (x_in, delta_t, C_dif, D_0, moments) |
| For test of the subroutine Bessel0_General only, returns the exact values of the moments of Bessel process Starting point +x_in, duration delta_t, coefficient C_dif, D_0 The tested subroutine is Bessel0_General from module BesselProcess, same notations INPUT: | |
| subroutine | RFOF_MeanExitTime0 (x_0, x_min, C_dif, Time_exit, ErrorFlag) |
| INPUT. | |
| subroutine | RFOF_MeanExitTime1 (a, x_0, b, relative_tolerance, C_dif, D_0, mean_first_exit_time, Error_Flag) |
| INPUT. | |
| subroutine | RFOF_MeanExitTime2 (a, x_0, b, relative_tolerance, C_dif, D_0, mean_first_exit_time) |
| INPUT. | |
| subroutine | RFOF_Bessel_0_move (a, x_init, b, max_duration, relative_tolerance, C_dif, D_0, duration, x_final, Error_Flag) |
| Main subroutine It performs repeated updates according to subroutine Bessel0_General,until x(t) exits the interval (a,b) with sufficient small time step such that the final point is not too far from the interval (a,b), so the linear approximation of the diffusion coefficient is still valid INPUT: | |
| subroutine | RFOF_Bessel_0_move_test (a, x_0, b, max_duration, relative_tolerance, C_dif, D_0, duration, x_final, ErrorFlag) |
| INPUT: | |
Contains exact results for the solution of the stochastic differential equation
![\[ dx(t)=2Cdt+2\sqrt(Cx(t))dw(t) \]](form_118.png)
where 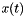 is proportional to the magnetic momentum, the constant
is proportional to the magnetic momentum, the constant 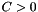 is related to the linear approximation of the diffusion coeeficient !coefficient
is related to the linear approximation of the diffusion coeeficient !coefficient 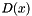 by the local approximation near
by the local approximation near 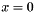 by
by
![\[D(x)=2Cx+O(x^2)\]](form_121.png)
The solution of this SDE is the square of the Bessel process of order 0 and can be represented as
![\[ x(t)=(w_1(Ct)+\sqrt(x_0))^2+(w_2(Ct))^2 \]](form_122.png)
where
![\[ w_1(t), \dots w_2(t)\]](form_123.png)
are independent standard Wiener processes and
![\[x_0=x(t=0)\]](form_124.png)
.
Contains exact results for the solution of the stochastic differential equation
![\[ dx(t)=2Cdt+2\sqrt(Cx(t))dw(t) \]](form_118.png)
![\[ dx(t)=dD(x)/dxdt+sqrt(D(x(t)))dw(t) \]](form_126.png)
In the case when we have a linear approximation
![\[D(x)=2C x+O(x^2) \]](form_127.png)
![\[ dx(t)=2Cdt+2\sqrt(Cx(t))dw(t) \]](form_118.png)
we have near 0
![\[ dx(t)=2Cdt+2\sqrt(Cx(t))dw(t) \]](form_118.png)
where 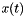 is proportional to the magnetic momentum, the constant
is proportional to the magnetic momentum, the constant 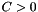 is related to the linear approximation of the diffusion coeeficient !coefficient
is related to the linear approximation of the diffusion coeeficient !coefficient 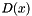 by the local approximation near
by the local approximation near 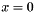 by
by
![\[D(x)=2Cx+O(x^2)\]](form_121.png)
The solution of this SDE is the square of the Bessel process of order 0 and can be represented as
![\[ x(t)=(w_1(Ct)+\sqrt(x_0))^2+(w_2(Ct))^2 \]](form_122.png)
where
![\[ w_1(t), \dots w_2(t)\]](form_123.png)
are independent standard Wiener processes and
![\[x_0=x(t=0)\]](form_124.png)
In the domain with x large, we use a general linear approximation for D(x)
![\[D(x)=2Cx+d +error \]](form_128.png)
and the update is given by a more general formula, derived from the previous
![\[ x(t)=(w_1(Ct)+\sqrt(x_0+d/(2C)))^2+(w_2(Ct))^2-d/(2C) \]](form_129.png)
We use the FORTRAN variable notations: 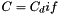 ,
, 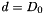 .
.
Contains exact results for the solution of the stochastic differential equation
![\[ dx(t)=2Cdt+2\sqrt(Cx(t))dw(t) \]](form_118.png)
![\[ dx(t)=dD(x)/dxdt+sqrt(D(x(t)))dw(t) \]](form_126.png)
In the case when we have a linear approximation
![\[D(x)=2C x+O(x^2) \]](form_127.png)
![\[ dx(t)=2Cdt+2\sqrt(Cx(t))dw(t) \]](form_118.png)
we have near 0
![\[ dx(t)=2Cdt+2\sqrt(Cx(t))dw(t) \]](form_118.png)
where 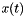 is proportional to the magnetic momentum, the constant
is proportional to the magnetic momentum, the constant 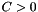 is related to the linear approximation of the diffusion coeeficient !coefficient
is related to the linear approximation of the diffusion coeeficient !coefficient 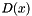 by the local approximation near
by the local approximation near 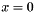 by
by
![\[D(x)=2Cx+O(x^2)\]](form_121.png)
The solution of this SDE is the square of the Bessel process of order 0 and can be represented as
![\[ x(t)=(w_1(Ct)+\sqrt(x_0))^2+(w_2(Ct))^2 \]](form_122.png)
where
![\[ w_1(t), \dots w_2(t)\]](form_123.png)
are independent standard Wiener processes and
![\[x_0=x(t=0)\]](form_124.png)
In the domain with x large, we use a general linear approximation for D(x)
![\[D(x)=2Cx+d +error \]](form_128.png)
and the update is given by a more general formula, derived from the previous
![\[ x(t)=(w_1(Ct)+\sqrt(x_0+d/(2C)))^2+(w_2(Ct))^2-d/(2C) \]](form_129.png)
.
Definition at line 19 of file RFOF_BesselProcess0.F90.
| subroutine RFOF_BesselProcess0::Bessel0 | ( | real(8), intent(in) | x_in, |
| real(8), intent(in) | delta_t, | ||
| real(8), intent(in) | C_dif, | ||
| real(8), intent(out) | x_fin | ||
| ) |
Subroutine Bessel0.
| [in] | x_in | Initial position |
| [in] | delta_t | The time interval |
| [in] | C_dif | From local aproximation:
|
| [out] | x_fin | The final position |
Definition at line 26 of file RFOF_BesselProcess0.F90.
| subroutine RFOF_BesselProcess0::exact_moments | ( | real(8), intent(in) | x_in, |
| real(8), intent(in) | delta_t, | ||
| real(8), intent(in) | C_dif, | ||
| real(8), dimension(max_moment_order), intent(out) | moments | ||
| ) |
For test of the subroutine Bessel0 only, returns the exact values of the moments of Bessel process Starting point +x_in, duration delta_t, coefficient C_dif The tested subroutine is Bessel0 from module BesselProcess, same notations.
Definition at line 46 of file RFOF_BesselProcess0.F90.
| subroutine RFOF_BesselProcess0::Bessel0 | ( | real(8), intent(in) | x_in, |
| real(8), intent(in) | delta_t, | ||
| real(8), intent(in) | C_dif, | ||
| real(8), intent(out) | x_fin | ||
| ) |
Subroutine Bessel0 Integration near x=0.
| [in] | x_in | initial position |
| [in] | delta_t | the time interval |
| [in] | C_dif | From local aproximation:
|
| [out] | x_fin | the final position |
Definition at line 37 of file RFOF_BesselProcess0_3.F90.
| subroutine RFOF_BesselProcess0::Bessel0_General | ( | real(8), intent(in) | x_in, |
| real(8), intent(in) | delta_t, | ||
| real(8), intent(in) | C_dif, | ||
| real(8), intent(in) | D_0, | ||
| real(8), intent(out) | x_fin | ||
| ) |
Integration, with local approximation of the diffusion coefficient
![\[D(x)=2*C_dif+D_0\]](form_130.png)
.
Definition at line 57 of file RFOF_BesselProcess0_3.F90.
| subroutine RFOF_BesselProcess0::exact_moments | ( | real(8), intent(in) | x_in, |
| real(8), intent(in) | delta_t, | ||
| real(8), intent(in) | C_dif, | ||
| real(8), dimension(max_moment_order), intent(out) | moments | ||
| ) |
For test of the subroutine Bessel0 only, returns the exact values of the moments of Bessel process Starting point +x_in, duration delta_t, coefficient C_dif The tested subroutine is Bessel0 from module BesselProcess, same notations.
Definition at line 95 of file RFOF_BesselProcess0_3.F90.
| subroutine RFOF_BesselProcess0::exact_momentsG | ( | real(8), intent(in) | x_in, |
| real(8), intent(in) | delta_t, | ||
| real(8), intent(in) | C_dif, | ||
| real(8), intent(in) | D_0, | ||
| real(8), dimension(max_moment_order), intent(out) | moments | ||
| ) |
For test of the subroutine Bessel0_General only, returns the exact values of the moments of Bessel process Starting point +x_in, duration delta_t, coefficient C_dif, D_0 The tested subroutine is Bessel0_General from module BesselProcess, same notations.
Definition at line 114 of file RFOF_BesselProcess0_3.F90.
| subroutine RFOF_BesselProcess0::Bessel0 | ( | real(8), intent(in) | x_in, |
| real(8), intent(in) | delta_t, | ||
| real(8), intent(in) | C_dif, | ||
| real(8), intent(out) | x_fin | ||
| ) |
Integration near x=0, when
![\[D(x)=2C_dif x+O(x^2) \]](form_133.png)
INPUT:
| x_in | initial pozition |
| delta_t | time step |
| C_dif | coeficient for local linear approximation of the diffusion coefficient OUTPUT: |
| x_fin | final pozition after time delta_t |
Definition at line 45 of file RFOF_BesselProcess0_5.F90.
| subroutine RFOF_BesselProcess0::Bessel0_General | ( | real(8), intent(in) | x_in, |
| real(8), intent(in) | delta_t, | ||
| real(8), intent(in) | C_dif, | ||
| real(8), intent(in) | D_0, | ||
| real(8), intent(out) | x_fin | ||
| ) |
Integration, with local approximation of the diffusion coefficient
![\[D(x)=2*C_dif+D_0\]](form_130.png)
The updates are performed according to exact solution of the squared Bessel process of order 0 INPUT:
| x_in | Initial pozition |
| delta_t | Time step |
| C_dif | Local linear approximation of the diffusion coefficient |
| D_0 | Coeficients for local linear approximation of the diffusion coefficient OUTPUT: |
| x_fin | Final pozition after time delta_t |
Definition at line 81 of file RFOF_BesselProcess0_5.F90.
| subroutine RFOF_BesselProcess0::exact_moments | ( | real(8), intent(in) | x_in, |
| real(8), intent(in) | delta_t, | ||
| real(8), intent(in) | C_dif, | ||
| real(8), dimension(max_moment_order), intent(out) | moments | ||
| ) |
For test of the subroutine Bessel0 only, returns the exact values of the moments of Bessel process Starting point +x_in, duration delta_t, coefficient C_dif The tested subroutine is Bessel0 from module BesselProcess, same notations INPUT:
| x_in | starting point of 0 order bessel process |
| delta_t | duration of Bessel procees |
| C_dif | From local aproximation:
|
| moments | 1 and 2 order moments of the Bessel process |
Definition at line 133 of file RFOF_BesselProcess0_5.F90.
| subroutine RFOF_BesselProcess0::exact_momentsG | ( | real(8), intent(in) | x_in, |
| real(8), intent(in) | delta_t, | ||
| real(8), intent(in) | C_dif, | ||
| real(8), intent(in) | D_0, | ||
| real(8), dimension(max_moment_order), intent(out) | moments | ||
| ) |
For test of the subroutine Bessel0_General only, returns the exact values of the moments of Bessel process Starting point +x_in, duration delta_t, coefficient C_dif, D_0 The tested subroutine is Bessel0_General from module BesselProcess, same notations INPUT:
| x_in | starting point of 0 order bessel process |
| delta_t | duration of Bessel procees |
| C_dif | From local aproximation: Diff_coef=2*C_dif*x OUTPUT: moments 1 and 2 order moments of the Bessel process |
Definition at line 164 of file RFOF_BesselProcess0_5.F90.
| subroutine RFOF_BesselProcess0::RFOF_MeanExitTime0 | ( | real(8), intent(in) | x_0, |
| real(8), intent(in) | x_min, | ||
| real(8), intent(in) | C_dif, | ||
| Real(8), intent(out) | Time_exit, | ||
| Integer, intent(out) | ErrorFlag | ||
| ) |
INPUT.
| a | |
| b | Endpoints of the interval |
| x_0 | starting point of 0 order Bessel process Admissible relative error |
| C_dif | From local aproximat:ion: Diff_coef=2*C_dif*x |
| mean_first_exit_time | The mean first exit time from (a,b) starting at x_0 |
| Error_Flag | ! zero when OK, 102 if not a<=x_0<=b, wrong ordering 103 if the diffusion coefficient is negative on interval (a,b) |
Definition at line 201 of file RFOF_BesselProcess0_5.F90.
| subroutine RFOF_BesselProcess0::RFOF_MeanExitTime1 | ( | real(8), intent(in) | a, |
| real(8), intent(in) | x_0, | ||
| real(8), intent(in) | b, | ||
| real(8), intent(in) | relative_tolerance, | ||
| real(8), intent(in) | C_dif, | ||
| real(8), intent(in) | D_0, | ||
| Real(8), intent(out) | mean_first_exit_time, | ||
| integer, intent(out) | Error_Flag | ||
| ) |
INPUT.
| a | |
| b | Endpoints of the interval |
| x_0 | starting point of 0 order Bessel process Admissible relative error |
| D_dif | |
| D_0 | From local aproximat:ion: Diff_coef=2*C_dif*x +D_0 |
| mean_first_exit_time | The mean first exit time from (a,b) starting at x_0 |
| Error_Flag | ! zero when OK, 102 if not a<=x_0<=b, wrong ordering 103 if the diffusion coefficient is negative on interval (a,b) |
Definition at line 241 of file RFOF_BesselProcess0_5.F90.
| subroutine RFOF_BesselProcess0::RFOF_MeanExitTime2 | ( | real(8), intent(in) | a, |
| real(8), intent(in) | x_0, | ||
| real(8), intent(in) | b, | ||
| real(8), intent(in) | relative_tolerance, | ||
| real(8), intent(in) | C_dif, | ||
| real(8), intent(in) | D_0, | ||
| Real(8), intent(out) | mean_first_exit_time | ||
| ) |
INPUT.
| a | |
| b | Endpoints of the interval |
| x_0 | starting point of 0 order Bessel process Admissible relative error |
| D_dif | |
| D_0 | From local aproximat:ion: Diff_coef=2*C_dif*x +D_0 |
| mean_first_exit_time | The mean first exit time from (a,b) starting at x_0 |
| Error_Flag | ! zero when OK, 102 if not a<=x_0<=b, wrong ordering 103 if the diffusion coefficient is negative on interval (a,b) Version of the previous subroutine No more test of the input data The test is performed at once in the calling subroutine |
Definition at line 327 of file RFOF_BesselProcess0_5.F90.
| subroutine RFOF_BesselProcess0::RFOF_Bessel_0_move | ( | real(8), intent(in) | a, |
| real(8), intent(in) | x_init, | ||
| real(8), intent(in) | b, | ||
| real(8), intent(in) | max_duration, | ||
| real(8), intent(in) | relative_tolerance, | ||
| real(8), intent(in) | C_dif, | ||
| real(8), intent(in) | D_0, | ||
| Real(8), intent(out) | duration, | ||
| real(8), intent(out) | x_final, | ||
| Integer, intent(out) | Error_Flag | ||
| ) |
Main subroutine It performs repeated updates according to subroutine Bessel0_General,until x(t) exits the interval (a,b) with sufficient small time step such that the final point is not too far from the interval (a,b), so the linear approximation of the diffusion coefficient is still valid INPUT:
---------------------------------------------------------------------------
| a | Endpoints of the interval |
| x_init | starting point of 0 order Bessel process |
| max_duration | The maximal time allowed |
| relative_tolerance | Admissible relative error |
| C_dif | |
| D_0 | From local linear aproximation: Diff_coef=2*C_dif*x +D_0 OUTPUT |
| duration | The approximate first exit time from (a,b) startin at x_0 |
| x_final | final position |
| Error_Flag | ErrorFlag=0 when a<=x_0<=b;ErrorFlag=102 When the Diffusionn coefficient is negative on (a,b), then Error_Flag=103 otherwise Error_Flag=0 |
Definition at line 405 of file RFOF_BesselProcess0_5.F90.
| subroutine RFOF_BesselProcess0::RFOF_Bessel_0_move_test | ( | real(8), intent(in) | a, |
| real(8), intent(in) | x_0, | ||
| real(8), intent(in) | b, | ||
| real(8), intent(in) | max_duration, | ||
| real(8), intent(in) | relative_tolerance, | ||
| real(8), intent(in) | C_dif, | ||
| real(8), intent(in) | D_0, | ||
| Real(8), intent(out) | duration, | ||
| real(8), intent(out) | x_final, | ||
| Integer, intent(out) | ErrorFlag | ||
| ) |
INPUT:
| a | Endpoints of the interval |
| x_init | starting point of 0 order Bessel process |
| max_duration | The maximal time allowed |
| relative_tolerance | Admissible relative error |
| C_dif | |
| D_0 | From local linear aproximation: Diff_coef=2*C_dif*x +D_0 OUTPUT |
| duration | The approximate first exit time from (a,b) startin at x_0 |
| x_final | final position |
| Error_Flag | ErrorFlag=0 when a<=x_0<=b;ErrorFlag=102 When the Diffusionn coefficient is negative on (a,b), then Error_Flag=103 otherwise Error_Flag=0 |
Definition at line 489 of file RFOF_BesselProcess0_5.F90.