Here are the data types with brief descriptions:

RFOF_kick::coeff_for_guiding_centre_kick	Coefficients defining the direction of the RF acceleration (for a single mode) in the configuration space 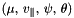$(\mu, \, v_\\|, \, \psi, \, \theta)$
diffusion_coef
diffusion_coef5
dum_magnetic_field	Dummy magnetic field for the standalone dummy-orbit test program for RFOF
dummy_orbit	Dummy-orbit code a standalone test program for RFOF
euitm_waves_interface	Interface to the EU-ITM data structure WAVES
dum_magnetic_field::magnetic_field_global	Parameters defining a simple magnetic field
RFOF_magnetic_field::magnetic_field_local	Defining all local magnetic field quantities needed by RFOF
RFOF_markers::particle	Structure including pointers to all quantities defining the Monte Carlo marker. Note that the pointers allows you to access the memory allocated for a different marker structure, e.g. by an orbit code which calls RFOF for inteaction with RF waves
RFOF_markers::particle_static	Structure including all quantities defining the Monte Carlo marker. Can be used to allocate memory which type::particle can point to. For detailed description see the definition of the fields, see type::particle
RFOF_resonance_memory::resonance_memory	Storage structure for for the memory of the resonance function. It has two purposes within RFOF:
RFOF_waves::rf_wave_global	Spline representation of the real part of the left hand polarized electric wave field
RFOF_waves::rf_wave_local	Structure including information about the local RF wave field
RFOF_waves::rf_wave_mode_global	Structure including information about the global RF wave field
RFOF_BesselProcess0	Contains exact results for the solution of the stochastic differential equation $dx(t)=2Cdt+2\sqrt(Cx(t))dw(t)$ where is proportional to the magnetic momentum, the constant is related to the linear approximation of the diffusion coeeficient !coefficient by the local approximation near by $D(x)=2Cx+O(x^2)$ The solution of this SDE is the square of the Bessel process of order 0 and can be represented as $x(t)=(w_1(Ct)+\sqrt(x_0))^2+(w_2(Ct))^2$ where $w_1(t), \dots w_2(t)$ are independent standard Wiener processes and $x_0=x(t=0)$
RFOF_constants	Module implementing the ITM physics constants
RFOF_diagnostics::RFOF_cumlative_diagnostics	Structure including all parameter defining the state of the time-integrated diagnostics in RFOF
RFOF_diagnostics	Module handling collection and storage of diagnostics in RFOF
RFOF_Efield_update	Module handling the normalisation of the electric wave field
RFOF_kick	Module handling wave acceleartion physics, i.e. the Monte Carlo kicks
RFOF_local_magnetic_field	Module for extracting local magnetic field information
RFOF_magnetic_field	Derived type and handling of the magnetic field
RFOF_main	Controls the workflow in RFOF
RFOF_markers	Module defining the properties of markers and and providing operations on markers
RFOF_mpi_module	Copied from (2011-04-19): http://solps-mdsplus.aug.ipp.mpg.de/wsvn/ASCOT/branches/asalmi/icmods/ascot/mpi_parallel.f90 and modified for RFOF
RFOF_numerics	Generic numerical solvers
RFOF_parameters	Collection of all parameters use in RFOF
RFOF_random_numbers	Random number generator for RFOF
RFOF_random_numbers_SG2	Random number generators for RFOF
RFOF_resonance_condition	Module handling resonance condition for wave particle interactions
RFOF_resonance_memory	Module handling the time memory of the resonance condition along the orbit, which allows time derivatives to be evaluated
RFOF_SpecialSolver	Contains subroutines for solutions of one dimesional stochastic differential equations
RFOF_SpecialSolver5	In RFOF_SpecialSolver5.f90 the regularization method 1 means reflection at X_MIN and X_MAX, the boundaries of the allowed domain. Contains subroutines for solution of one dimesional stochastic differential equation for Monte-Carlo simulation of RF heating: $dx(t)=D'(x)dt+\sqrt(2 D(x)) dw(t)$ In this version we use a combination of 2 integration methods. Both integration methods use 3 kind of treating of the singularity at x=0,called regularization methods. Regularization method 0 means no regularization The test is performed by comparing the result with a simplest Euler method in the case of an artificial form of the diffusion coefficient. These methods are addaptive: the time step size is modified according to a prescribed relative tolerance In this version the program is stopped, with suitable error message, in the case when the required relative error cannot be attained in a resonable time Two integration methods are used. The input is the the function , the diffusion coefficient. The function is computed in 3 points.The 3 points are selected such that the best linear approximation of $\sigma(x)=\sqrt(2 D(x))$ , has a relative tolerance less then a given input relative error In both integration methods a local linear approximation of $\sqrt(D(x))$ , according to given input relative tollerance is generated. In the method 1 the exact solution of the approximate linear equation is used for update, we have a strong 1/2 order method This method is usefull near , no assumptions are made on higer order derivatives. In the integration method 2 an extrapolation is performed, by using the same information on : a quadratic approximation of $\sqrt(D(x))$ is generated an from this approximation the analytic form of the derivatives of the terms of SDE are generated, that are used to generate a strong 3/2 order stochastic integrator. This is recomended to use for larger values of x. The main problem is the that near the term $\sqrt(D(x))$ is not differentiable, so a regularization is needed. Two regularization methods are used, for both integration methods, method 1 and method 2. In the our notatation regularization method 0 means no regularization. In the regularization method 1 when $x(t)<X\_MIN$ or $x(t)>X\_MAX$ , then $x(t)->2X\_MIN-x(t)$ , or $x(t)->2X\_MIN-x(t)$ (subroutine Correction_domain_boundary ). Method 2 use an input small parameter,reg_param_diff_coef, that is small compared to the typical mean value of the diffusion coefficient ( see below) . In the regularization method 2, the behavior near x=0 , is modified: the function is replaced by $\sqrt( D(x)^2+reg\_param\_diff\_coef^2)$ The parameter reg_param_diff_coef is defined in the term of the input parameter mean_diff_coef, that is an estimate of the typical order of magnitude of the diffusion coefficient, and the parameter small_adimensional_diff_coef_fact that can be chosen related to the imposed relative Monte-Carlo tolerance. TO DO: Computation of the cutoff parameters $X\_MAX$ , $X\_MIN$ introduced, in order to define the allowed domain of motion. call diffusion_coefficient4(x,diff_coeficient,Error_flag), used for test, to be replaced by RFOF module
RFOF_types::RFOF_state	State of RFOF structure. The state includes:
RFOF_stochastics	Random number generators for RFOF
RFOF_types	Module for composite derived types
RFOF_waves	Module handling the RF wave fields
RFOF_wiener_sample_paths	Module handling samples of Wiener processes (Brownain sample paths) The sample path is stored in a type Wiener_process_sample_path. The time grid use is stored in reversed order, i.e. the starting-time is stored in the last occupied element of the time vector, while the end-time is stored in the first element. This ordering optimizes the use within Monte Carlo codes with adaptive time stepping, in which you often wish to refine the next upcoming time step. With the reversed ordering the "next upcoming time step" is at the end of the vector, thus adding a time point will only require changes to the last few elements of the time-vectors
RFOF_parameters::rz_boundingbox	Bounding box for the plasma and vacuume regions
RFOF_wiener_sample_paths::Wiener_process_sample_path	Samples from the Wiener process