RFOF - RF Library for Orbit Following Codes
Public Member Functions
RFOF_stochastics Module Reference

Random number generators for RFOF. More...

List of all members.

Public Member Functions

subroutine Standard_map (p, q, nr_iterations)
 A version of the Standard-map is implemented, to realize decorrelation of the seeds of random number generators on different nodes. The input parameters: nr_iterations and map_parameter must be set dependent on the mpi_rank of the node. The uniform input-output random variables (x,y) and the system_clock outputs can be used to generate the seeds of the uniform ranom number generators Standard map for particular value of the parameter 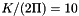$K/(2\Pi)=10$ In this case the behavior is chaotic. Input:
subroutine init_RANDOM_NUMBER (init_mode, init_parameter1, init_parameter2)
 Initialiation of the intrinsic random number generator RANDOM_NUMBER() by using the subroutine system_clock( , ,) and the standard map Input.
subroutine init_RM48 (init_mode, init_parameter1, init_parameter2)
 Initialiation of the universal random number generator RM48() by using the subroutine system_clock( , ,) and the standard map Input.
subroutine gaussian_random_vectorRM48 (grw)
 Subroutine gaussian_random_vector(grw) The algorithm is a modification of the polar method The algorithm is from the book: P.E. Kloeden, E. Platten, "Numerical solution of stochastic differential equations", page 13 The uniform random number generator is RM48.
subroutine gaussian_random_vector (grw)
 Subroutine gaussian_random_vector(grw) The algorithm is a modification of the polar method The algorithm is from the book: P.E. Kloeden, E. Platten, "Numerical solution of stochastic differential equations", page 13 The uniform random number generator is the intrinsic Random_Numbers()
subroutine Marsaglia_Bray_RM48 (X)
 Normal generator of Marsaglia and Bray (1964), for details see: Luc Devroye, "Non-uniform random variate generation", Springer, 1986, page 390, chapter IX Generate N(0,1) random number. The uniform random number generator is RM48 Output:
subroutine MarsagliaBray (X)
 Normal generator of Marsaglia and Bray (1964), for details see: Luc Devroye, "Non-uniform random variate generation", Springer, 1986, page 390, chapter IX The uniform random number generator is intrinsic Random_Number() Generate N(0,1) random number. Output:
subroutine Correlated_Gauss_Gen (delta_t, normal_vect, delta_w, delta_Z)
 Generate pair of Gaussian variables (delta_w,delta_Z ) that is a Wiener process w(t) and 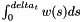$ \int_{0}^{delta_t}w(s)ds $ These variables are used in the stochastic integrators.
subroutine PolarGaussAccuracyTest1 (nit, init_mode, init_parameter1, init_parameter2)
 END OF WORKING SUBROUTINES.
subroutine MarsagliaBrayAccuracyTest1 (nit, init_mode, init_parameter1, init_parameter2)
 subroutine MarsagliaBrayAccuracyTest1( nit,init_mode, init_parameter1,& &init_parameter2) The correctness of the Gaussian random number generator is tested. from subroutine Marsaglia_Bray_RM48(X) In this version the random number generator uses the Marsaglia-Bray method and the portable RM48 uniform random number generator Input:
subroutine PolarGaussSpeedTest1 (nit, init_mode, init_parameter1, init_parameter2)
 Comparative speed tests:RM48 and intrinsic random number generators.
subroutine MarsagliaBraySpeedTest1 (nit, init_mode, init_parameter1, init_parameter2)
 The speed of the Gaussian random number generator is tested. from subroutine Marsaglia_Bray_RM48(X) In this version the random number generator uses the Marsaglia-Bray method and the portable RM48 uniform random number generator Input:
subroutine PolarGaussAccuracyTest2 (nit, init_mode, init_parameter1, init_parameter2)
 Accuracy tests by using the intrinsic random number generator.
subroutine MarsagliaBrayAccuracyTest2 (nit, init_mode, init_parameter1, init_parameter2)
 The correctness of the Gaussian random number generator is tested. from subroutine Marsaglia_Bray(X) In this version the random number generator uses the Marsaglia-Bray method and the intrinsic RANDOM_NUMBER uniform random number generator Input:
subroutine PolarGaussSpeedTest2 (nit, init_mode, init_parameter1, init_parameter2)
 Speed tests by using the intrinsic random number generator.
subroutine MarsagliaBraySpeedTest2 (nit, init_mode, init_parameter1, init_parameter2)
 The speed of the Gaussian random number generator is tested. from subroutine Marsaglia_Bray(X) In this version the random number generator uses the Marsaglia-Bray method and the intrinsic RANDOM_NUMBER uniform random number generator Input:
subroutine correlated_GaussTest (nit, init_mode, init_parameter1, init_parameter2)
 Test of the subroutine Correlated_Gauss_Gen(delta_t, normal_vector, delta_w, delta_Z ) &init_parameter2) In this version the random number generator uses the polar method and the portable RM48 uniform random number generator Input:

Detailed Description

Random number generators for RFOF.

Initialization of uniform random number generators Exact Gaussian random number generators

Author:
Gyorgy Steinbrecher, EURATOM-MEdC
Date:
2011.07.11
Version:
"$Id: RFOF_stochastics.F90 188 2011-09-12 11:50:22Z tjohnson $"

Added subroutines: for initialization init_RM48() of the uniform random number generator RM48 and for the initialization of the intrinsec uniform random number generator RANDOM_NUMBER. Generators for scalar and vector Gaussian random variables are added. Random number generator based on the Standard map is used to generate distinct seed for the initialization of the uniform random number generators on the distinct node, to avoid possible correlations of the random number generators on the different nodes

Definition at line 18 of file RFOF_stochastics.F90.

Member Function/Subroutine Documentation

subroutine RFOF_stochastics::Standard_map ( real(8), intent(inout)  p,
real(8), intent(inout)  q,
integer, intent(in)  nr_iterations 
)

A version of the Standard-map is implemented, to realize decorrelation of the seeds of random number generators on different nodes. The input parameters: nr_iterations and map_parameter must be set dependent on the mpi_rank of the node. The uniform input-output random variables (x,y) and the system_clock outputs can be used to generate the seeds of the uniform ranom number generators Standard map for particular value of the parameter 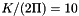$K/(2\Pi)=10$ In this case the behavior is chaotic. Input:

Parameters:
nr_iterationsNumber of iterationns of teh standard map Input-output:
qAngular coordinate, normalized to 1
pAngular momentum, in this version modulo 1

Definition at line 41 of file RFOF_stochastics.F90.

subroutine RFOF_stochastics::init_RANDOM_NUMBER ( integer(4), intent(in)  init_mode,
real(8), intent(in)  init_parameter1,
real(8), intent(in)  init_parameter2 
)

Initialiation of the intrinsic random number generator RANDOM_NUMBER() by using the subroutine system_clock( , ,) and the standard map Input.

Parameters:
init_modeIf init_mode/=0, then the reproducible initialization seed is given by the 'init_parameter1, init_parameter2'. Else if init_mode=0, the seed is generated by the local parameter ic4 returned by 'system_clock' and modified by the use of the standard map according to the parameters init_parameter1, init_parameter2.
init_parameter1Node-dependent, used for initial value for standard map
init_parameter2Node dependent, used for initial value for standard map

Definition at line 79 of file RFOF_stochastics.F90.

subroutine RFOF_stochastics::init_RM48 ( integer(4), intent(in)  init_mode,
real(8), intent(in)  init_parameter1,
real(8), intent(in)  init_parameter2 
)

Initialiation of the universal random number generator RM48() by using the subroutine system_clock( , ,) and the standard map Input.

Parameters:
init_modeIf init_mode/=0, then the reproducible initialization seed is given by the 'init_parameter1, init_parameter2'. Else if init_mode=0, the seed is generated by the local parameter ic4 returned by 'system_clock' and modified by the use of the standard map according to the parameters init_parameter1, init_parameter2.
init_parameter1Node-dependent, used for initial value for standard map
init_parameter2Node dependent, used for initial value for standard map

Definition at line 140 of file RFOF_stochastics.F90.

subroutine RFOF_stochastics::gaussian_random_vectorRM48 ( real(8), dimension(2), intent(out)  grw)

Subroutine gaussian_random_vector(grw) The algorithm is a modification of the polar method The algorithm is from the book: P.E. Kloeden, E. Platten, "Numerical solution of stochastic differential equations", page 13 The uniform random number generator is RM48.

Output:

Parameters:
grw2 dimensional N(0,1) vector with independent components.

Definition at line 185 of file RFOF_stochastics.F90.

subroutine RFOF_stochastics::gaussian_random_vector ( real(8), dimension(2), intent(out)  grw)

Subroutine gaussian_random_vector(grw) The algorithm is a modification of the polar method The algorithm is from the book: P.E. Kloeden, E. Platten, "Numerical solution of stochastic differential equations", page 13 The uniform random number generator is the intrinsic Random_Numbers()

Output:

Parameters:
grw2 dimensional N(0,1) vector with independent components. Subroutine gaussian_random_vector(grw) The algorithm is a modification of the polar method returns : grw, automatically 2 dimensional N(0,1) vector. The comonents are independent.It is usefull whenewer large number of N(0,1) are needed generate a pair of independent N(0,1) real(8) The algorithm is from: P.E. Kloeden, E. Platten, "Numerical solution of stochastic differential equations", page 13 The uniform random number generator is the intrinsic Random_Number()

Definition at line 228 of file RFOF_stochastics.F90.

subroutine RFOF_stochastics::Marsaglia_Bray_RM48 ( real(8), intent(out)  X)

Normal generator of Marsaglia and Bray (1964), for details see: Luc Devroye, "Non-uniform random variate generation", Springer, 1986, page 390, chapter IX Generate N(0,1) random number. The uniform random number generator is RM48 Output:

Parameters:
XN(0,1) random number

Definition at line 261 of file RFOF_stochastics.F90.

subroutine RFOF_stochastics::MarsagliaBray ( real(8), intent(out)  X)

Normal generator of Marsaglia and Bray (1964), for details see: Luc Devroye, "Non-uniform random variate generation", Springer, 1986, page 390, chapter IX The uniform random number generator is intrinsic Random_Number() Generate N(0,1) random number. Output:

Parameters:
XN(0,1) random number

Definition at line 329 of file RFOF_stochastics.F90.

subroutine RFOF_stochastics::Correlated_Gauss_Gen ( real(8), intent(in)  delta_t,
real(8), dimension(2), intent(in)  normal_vect,
real(8), intent(out)  delta_w,
real(8), intent(out)  delta_Z 
)

Generate pair of Gaussian variables (delta_w,delta_Z ) that is a Wiener process w(t) and 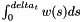$ \int_{0}^{delta_t}w(s)ds $ These variables are used in the stochastic integrators.

differential equations", page 352, Eq. 4.3. Notations are preserved The N(0,1) random number generator is gaussian_random_vectorRM48(grw), the uniform pseudo random number generator is RM48() Input:

Parameters:
delta_tThe time step in the stochastic integrator param normal_vect Random normal 2 dim vector, independent components Output
delta_wRandom Gaussiam variable
delta_ZRandom Gaussian variable The properties of delta_w and delta_W are the following: 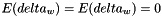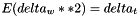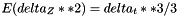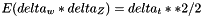$E(delta_w)=E(delta_w)=0$ $E(delta_w**2)=delta_t$ $E(delta_Z**2)=delta_t**3/3$ $E(delta_w*delta_Z)=delta_t**2/2$

Definition at line 412 of file RFOF_stochastics.F90.

subroutine RFOF_stochastics::PolarGaussAccuracyTest1 ( real(8), intent(in)  nit,
integer(4), intent(in)  init_mode,
real(8), intent(in)  init_parameter1,
real(8), intent(in)  init_parameter2 
)

END OF WORKING SUBROUTINES.

----------------------------------------------------------------------------------------- Follows Subroutines for the test of the Gaussian random number generators Comparative test of the Marsaglia_Bray(1964) generator and the polar method, combined with random number generators: RM48 and the intrinsic generator RANDOM_NUMBER Accuracy tests by using the RM48 uniform random number generator &init_parameter2) The correctness of the Gaussian random number generator is tested from subroutine gaussian_random_vectorRM48(grw) In this version the random number generator uses the polar method and the portable RM48 uniform random number generator Input:

Parameters:
nitNumber of iterations
init_modeIf init_mode/=0, then the reproducible initialization seed is given by the 'init_parameter1, init_parameter2'. Else if init_mode=0, the seed is generated by the local parameter ic4 returned by 'system_clock' and modified by the use of the standard map according to the parameters init_parameter1, init_parameter2.
init_parameter1Node-dependent, used for initial value for standard map
init_parameter2Node dependent, used for initial value for standard map The output is printed and it is self explanatory
[in]nitNumber of iterations

Definition at line 468 of file RFOF_stochastics.F90.

subroutine RFOF_stochastics::MarsagliaBrayAccuracyTest1 ( real(8), intent(in)  nit,
integer(4), intent(in)  init_mode,
real(8), intent(in)  init_parameter1,
real(8), intent(in)  init_parameter2 
)

subroutine MarsagliaBrayAccuracyTest1( nit,init_mode, init_parameter1,& &init_parameter2) The correctness of the Gaussian random number generator is tested. from subroutine Marsaglia_Bray_RM48(X) In this version the random number generator uses the Marsaglia-Bray method and the portable RM48 uniform random number generator Input:

Parameters:
nitNumber of iterations
init_modeIf init_mode/=0, then the reproducible initialization seed is given by the 'init_parameter1, init_parameter2'. Else if init_mode=0, the seed is generated by the local parameter ic4 returned by 'system_clock' and modified by the use of the standard map according to the parameters init_parameter1, init_parameter2.
init_parameter1Node-dependent, used for initial value for standard map
init_parameter2Node dependent, used for initial value for standard map The output is printed and it is self explanatory

Definition at line 536 of file RFOF_stochastics.F90.

subroutine RFOF_stochastics::PolarGaussSpeedTest1 ( real(8), intent(in)  nit,
integer(4), intent(in)  init_mode,
real(8), intent(in)  init_parameter1,
real(8), intent(in)  init_parameter2 
)

Comparative speed tests:RM48 and intrinsic random number generators.

Speed tests, using the RM48 uniform random number generator The speed of the Gaussian random number generator is tested. from subroutine gaussian_random_vectorRM48(grw) In this version the random number generator uses the polar method and the portable RM48 uniform random number generator Input:

Parameters:
nitNumber of iterations
init_modeIf init_mode/=0, then the reproducible initialization seed is given by the 'init_parameter1, init_parameter2'. Else if init_mode=0, the seed is generated by the local parameter ic4 returned by 'system_clock' and modified by the use of the standard map according to the parameters init_parameter1, init_parameter2.
init_parameter1Node-dependent, used for initial value for standard map
init_parameter2Node dependent, used for initial value for standard map The output is printed and it is self explanatory

Definition at line 609 of file RFOF_stochastics.F90.

subroutine RFOF_stochastics::MarsagliaBraySpeedTest1 ( real(8), intent(in)  nit,
integer(4), intent(in)  init_mode,
real(8), intent(in)  init_parameter1,
real(8), intent(in)  init_parameter2 
)

The speed of the Gaussian random number generator is tested. from subroutine Marsaglia_Bray_RM48(X) In this version the random number generator uses the Marsaglia-Bray method and the portable RM48 uniform random number generator Input:

Parameters:
nitNumber of iterations
init_modeIf init_mode/=0, then the reproducible initialization seed is given by the 'init_parameter1, init_parameter2'. Else if init_mode=0, the seed is generated by the local parameter ic4 returned by 'system_clock' and modified by the use of the standard map according to the parameters init_parameter1, init_parameter2.
init_parameter1Node-dependent, used for initial value for standard map
init_parameter2Node dependent, used for initial value for standard map The output is printed and it is self explanatory

Definition at line 661 of file RFOF_stochastics.F90.

subroutine RFOF_stochastics::PolarGaussAccuracyTest2 ( real(8), intent(in)  nit,
integer(4), intent(in)  init_mode,
real(8), intent(in)  init_parameter1,
real(8), intent(in)  init_parameter2 
)

Accuracy tests by using the intrinsic random number generator.

The correctness of the Gaussian random number generator is tested. from subroutine gaussian_random_vector(grw) In this version the random number generator uses the polar method and the intrinsic RANDOM_NUMBER uniform random number generator Input:

Parameters:
nitNumber of iterations
init_modeIf init_mode/=0, then the reproducible initialization seed is given by the 'init_parameter1, init_parameter2'. Else if init_mode=0, the seed is generated by the local parameter ic4 returned by 'system_clock' and modified by the use of the standard map according to the parameters init_parameter1, init_parameter2.
init_parameter1Node-dependent, used for initial value for standard map
init_parameter2Node dependent, used for initial value for standard map The output is printed and it is self explanatory

Definition at line 712 of file RFOF_stochastics.F90.

subroutine RFOF_stochastics::MarsagliaBrayAccuracyTest2 ( real(8), intent(in)  nit,
integer(4), intent(in)  init_mode,
real(8), intent(in)  init_parameter1,
real(8), intent(in)  init_parameter2 
)

The correctness of the Gaussian random number generator is tested. from subroutine Marsaglia_Bray(X) In this version the random number generator uses the Marsaglia-Bray method and the intrinsic RANDOM_NUMBER uniform random number generator Input:

Parameters:
nitNumber of iterations
init_modeIf init_mode/=0, then the reproducible initialization seed is given by the 'init_parameter1, init_parameter2'. Else if init_mode=0, the seed is generated by the local parameter ic4 returned by 'system_clock' and modified by the use of the standard map according to the parameters init_parameter1, init_parameter2.
init_parameter1Node-dependent, used for initial value for standard map
init_parameter2Node dependent, used for initial value for standard map The output is printed and it is self explanatory

Definition at line 776 of file RFOF_stochastics.F90.

subroutine RFOF_stochastics::PolarGaussSpeedTest2 ( real(8), intent(in)  nit,
integer, intent(in)  init_mode,
real(8), intent(in)  init_parameter1,
real(8), intent(in)  init_parameter2 
)

Speed tests by using the intrinsic random number generator.

The speed of the Gaussian random number generator is tested. from subroutine gaussian_random_vector(grw) In this version the random number generator uses the polar method and the intrinsic RANDOM_NUMBER uniform random number generator Input:

Parameters:
nitNumber of iterations
init_modeIf init_mode/=0, then the reproducible initialization seed is given by the 'init_parameter1, init_parameter2'. Else if init_mode=0, the seed is generated by the local parameter ic4 returned by 'system_clock' and modified by the use of the standard map according to the parameters init_parameter1, init_parameter2.
init_parameter1Node-dependent, used for initial value for standard map
init_parameter2Node dependent, used for initial value for standard map The output is printed and it is self explanatory

Definition at line 847 of file RFOF_stochastics.F90.

subroutine RFOF_stochastics::MarsagliaBraySpeedTest2 ( real(8), intent(in)  nit,
integer(4), intent(in)  init_mode,
real(8), intent(in)  init_parameter1,
real(8), intent(in)  init_parameter2 
)

The speed of the Gaussian random number generator is tested. from subroutine Marsaglia_Bray(X) In this version the random number generator uses the Marsaglia-Bray method and the intrinsic RANDOM_NUMBER uniform random number generator Input:

Parameters:
nitNumber of iterations
init_modeIf init_mode/=0, then the reproducible initialization seed is given by the 'init_parameter1, init_parameter2'. Else if init_mode=0, the seed is generated by the local parameter ic4 returned by 'system_clock' and modified by the use of the standard map according to the parameters init_parameter1, init_parameter2.
init_parameter1Node-dependent, used for initial value for standard map
init_parameter2Node dependent, used for initial value for standard map The output is printed and it is self explanatory

Definition at line 896 of file RFOF_stochastics.F90.

subroutine RFOF_stochastics::correlated_GaussTest ( real(8), intent(in)  nit,
integer(4), intent(in)  init_mode,
real(8), intent(in)  init_parameter1,
real(8), intent(in)  init_parameter2 
)

Test of the subroutine Correlated_Gauss_Gen(delta_t, normal_vector, delta_w, delta_Z ) &init_parameter2) In this version the random number generator uses the polar method and the portable RM48 uniform random number generator Input:

Parameters:
nitNumber of iterations
init_modeIf init_mode/=0, then the reproducible initialization seed is given by the 'init_parameter1, init_parameter2'. Else if init_mode=0, the seed is generated by the local parameter ic4 returned by 'system_clock' and modified by the use of the standard map according to the parameters init_parameter1, init_parameter2.
init_parameter1Node-dependent, used for initial value for standard map
init_parameter2Node dependent, used for initial value for standard map The output is printed and it is self explanatory

Definition at line 948 of file RFOF_stochastics.F90.

The documentation for this module was generated from the following file: