 |
RFOF - RF Library for Orbit Following Codes
|
 |
RFOF - RF Library for Orbit Following Codes
|
Contains subroutines for solutions of one dimesional stochastic differential equations. More...
Public Member Functions | |
| logical function | aprox_equal (x, y) |
Return true if the relative error of 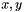 is less then the internal eror. CAUTION: Must be used ONLYin situations when the aproximate equality of is less then the internal eror. CAUTION: Must be used ONLYin situations when the aproximate equality of 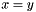 must be detected, x, y perturbed by round-off errors AND neither must be detected, x, y perturbed by round-off errors AND neither 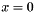 or or 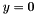 occur, like in the subroutines below, where the actual relative error is generated by floating point round-off. occur, like in the subroutines below, where the actual relative error is generated by floating point round-off. | |
| subroutine | RFOF_sigma (x, sigma, Error_flag) |
The relation to the diffusion coefficient is: 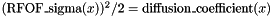 . . | |
| subroutine | linear_fit (x, y, A, B, ser) |
Linear fit : 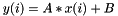 ; ; 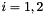 . Returns the coefficients. . Returns the coefficients. | |
| subroutine | linear_aprox_minmax (x, y, A, B, minmaxerr, ser) |
Find the best min-max approximation of the 3 points with coordinates ![$[x(i), y(i)]$](form_75.png) , , 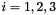 , by linear function , by linear function 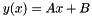 .Returns the coefficients .Returns the coefficients 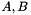 and the relative error and the error signal. For 3 points the minmax fit is computed more quicly compared to the least square fit. and the relative error and the error signal. For 3 points the minmax fit is computed more quicly compared to the least square fit. | |
| subroutine | linear_aprox_minmax2 (xc, delta, y, A, B, minmaxerr, ser) |
In the degenerate case, when the order is different from 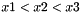 , then ser=8 In the normal case ser=0. , then ser=8 In the normal case ser=0. | |
| subroutine | quadratic_interpolation (xc, delta_x, y, a, b, c, ser) |
In the degenerate case, when the order is different from 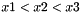 , then ser=8 In the normal case ser=0. , then ser=8 In the normal case ser=0. | |
| subroutine | RFOF_exact_solution (lambda, x_in, delta_t, W, A, B, x_fin, ser) |
| Try to detect anomaly. | |
| subroutine | reflect (miror, object_image) |
| The exponent must be infinitesimal. | |
| subroutine | RFOF_one_step_generalcase (method, x_min, delta_t_in, x_in, tolerance, delta_t_out, x_fin, output_error, ser) |
| Object/image position. | |
| subroutine | RFOF_SDE_integrator_corection (x_min, x_in, delta_x, sigma, dt, x_final, ser) |
| Not probable, but be sure. | |
| subroutine | RFOF_multi_step_generalcase (method, x_min, delta_t_in, delta_t_out, x_in, x_fin, time_in, time_fin, T_max, tolerance, ser) |
| We use the approximation $(x)=(DiffCoef(x)=mx^2+nx+p)$. | |
| subroutine | RFOF_boundary_ymin (d_prime, y_min) |
| Approximation, works because the singularity of stationary PDF is logarithmic. | |
| subroutine | RFOF_multi_step_boundarycase (y_min, y_max, delta_t_in, y_in, time_in, T_max, tolerance, delta_t_out, y_fin, time_fin, ser) |
| Solution of the ITO SDE $dy=-0.5(y) dw(t)$ in the domain $0<x<lin_apprx_lim$ or $y>(lin_apprx_lim)/2-(d')=y_{min}$ The variables x and y are related by $x=d'^{2}(-2y)$. The constant d' is defined by the linear approximation of the diffusion coefficient D(x) for 0<x<linearity_approx_limit: $D(x)=d'^2*x/2$ The logarithmic singularity in the x variable at x=0 is regularized. The asymptotic form of the stationary distibution function in new variable y is $(y)=y(-2y)$ The initial value of the time t is t_in, the initial value of the y(t) is y_in The trajectory y(t) is computed while the time (with initial value t_in) is less then T_max, and y(t)<logarithm of the linearity_approx_limit. The time step is adapted such that the relative error is less then the input relative error, denoted "tolerance". | |
| subroutine | RFOF_one_step_boundarycase (y_max, delta_t, normal_vector, y_in, y_fin, error) |
| The time step delta_t si decreased at most by a factor 2**maxdivision. | |
| real(8) function | exact_moments (x) |
| Subroutines for testing. | |
| subroutine | multi_step_boundarytest1 (ntraject) |
| subroutine | boundarytest1_Euler (y_min, y_max, y_in, y_fin, t_in, t_fin, ndivision, escape) |
| End of main loop. | |
| subroutine | multi_step_generaltest3 (ntraject) |
Test the solver for the SDE 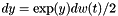 , by computing mean values in stationary state and comparing with the exact values given by simpest Euler method Test of subroutine RFOF_multi_step_boundarycase for , by computing mean values in stationary state and comparing with the exact values given by simpest Euler method Test of subroutine RFOF_multi_step_boundarycase for  . . | |
| subroutine | generaltest3_Euler (x_min, x_in, x_fin, t_in, t_fin, ndivision, ser) |
Simple Euler-Maruyana solver for the SDE 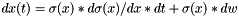 where where 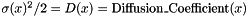 . . | |
Contains subroutines for solutions of one dimesional stochastic differential equations.
Definition at line 8 of file RFOF_SpecialSolver.F90.
| logical function RFOF_SpecialSolver::aprox_equal | ( | real(8), intent(in) | x, |
| real(8), intent(in) | y | ||
| ) |
Return true if the relative error of 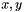 is less then the internal eror. CAUTION: Must be used ONLYin situations when the aproximate equality of
is less then the internal eror. CAUTION: Must be used ONLYin situations when the aproximate equality of 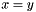 must be detected, x, y perturbed by round-off errors AND neither
must be detected, x, y perturbed by round-off errors AND neither 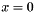 or
or 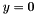 occur, like in the subroutines below, where the actual relative error is generated by floating point round-off.
occur, like in the subroutines below, where the actual relative error is generated by floating point round-off.
Definition at line 22 of file RFOF_SpecialSolver.F90.
| subroutine RFOF_SpecialSolver::RFOF_sigma | ( | real(8), intent(in) | x, |
| real(8), intent(out) | sigma, | ||
| integer, intent(out) | Error_flag | ||
| ) |
The relation to the diffusion coefficient is: 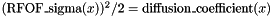 .
.
| [out] | Error_Flag | Error_Flag denoted also by "ser" in the following: Error_Flag=0 normal case. Error_Flag=9 for wrog value(negative) of the diffusion coefficinet Error_Flag=10 for anomalous return from the diffusion coefficient routine |
Definition at line 42 of file RFOF_SpecialSolver.F90.
| subroutine RFOF_SpecialSolver::linear_fit | ( | real(8), dimension(2), intent(in) | x, |
| real(8), dimension(2), intent(in) | y, | ||
| real(8), intent(out) | A, | ||
| real(8), intent(out) | B, | ||
| integer, intent(out) | ser | ||
| ) |
Linear fit : 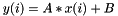 ;
; 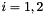 . Returns the coefficients.
. Returns the coefficients.
| [out] | ser | In the degenerate case, when the order is different from 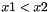 , then ser=8. In the normal case ser=0 , then ser=8. In the normal case ser=0 |
Definition at line 65 of file RFOF_SpecialSolver.F90.
| subroutine RFOF_SpecialSolver::linear_aprox_minmax | ( | real(8), dimension(3), intent(in) | x, |
| real(8), dimension(3), intent(in) | y, | ||
| real(8), intent(out) | A, | ||
| real(8), intent(out) | B, | ||
| real(8), intent(out) | minmaxerr, | ||
| integer, intent(out) | ser | ||
| ) |
Find the best min-max approximation of the 3 points with coordinates ![$[x(i), y(i)]$](form_75.png) ,
, 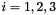 , by linear function
, by linear function 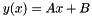 .Returns the coefficients
.Returns the coefficients 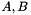 and the relative error and the error signal. For 3 points the minmax fit is computed more quicly compared to the least square fit.
and the relative error and the error signal. For 3 points the minmax fit is computed more quicly compared to the least square fit.
Definition at line 88 of file RFOF_SpecialSolver.F90.
| subroutine RFOF_SpecialSolver::linear_aprox_minmax2 | ( | real(8), intent(in) | xc, |
| real(8), intent(in) | delta, | ||
| real(8), dimension(3), intent(in) | y, | ||
| real(8), intent(out) | A, | ||
| real(8), intent(out) | B, | ||
| real(8), intent(out) | minmaxerr, | ||
| integer, intent(out) | ser | ||
| ) |
In the degenerate case, when the order is different from 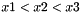 , then ser=8 In the normal case ser=0.
, then ser=8 In the normal case ser=0.
The same as the previous subroutine linear_aprox_minmax, but in this case the x points are equidistants Their coordinates are: 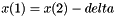 ;
; 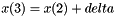 ; We denoted:
; We denoted: 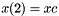 Find the best min-max approximation of the 3 points with coordinates
Find the best min-max approximation of the 3 points with coordinates ![$[x(i), y(i)]$](form_75.png) ,
, 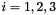 , by linear function
, by linear function 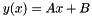 .Returns the coefficients
.Returns the coefficients 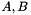 and the relative error and the error signal. For 3 points the minmax fit is computed more quicly compared to the least square fit
and the relative error and the error signal. For 3 points the minmax fit is computed more quicly compared to the least square fit
Definition at line 123 of file RFOF_SpecialSolver.F90.
| subroutine RFOF_SpecialSolver::quadratic_interpolation | ( | real(8), intent(in) | xc, |
| real(8), intent(in) | delta_x, | ||
| real(8), dimension(3), intent(in) | y, | ||
| real(8), intent(out) | a, | ||
| real(8), intent(out) | b, | ||
| real(8), intent(out) | c, | ||
| integer, intent(out) | ser | ||
| ) |
In the degenerate case, when the order is different from 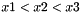 , then ser=8 In the normal case ser=0.
, then ser=8 In the normal case ser=0.
Quadratic interpolation 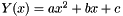 of the values of the array
of the values of the array 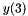 in the
in the 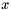 points, given by the array
points, given by the array 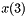 , where the points
, where the points 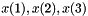 that are equidistants Their coordinates are:
that are equidistants Their coordinates are: 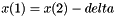 ;
; 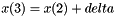 ; We denoted the centrak point:x(2)=xc Find the polinomial interpolation of the 3 points with coordinates
; We denoted the centrak point:x(2)=xc Find the polinomial interpolation of the 3 points with coordinates ![$[x(i), y(i)]$](form_75.png) ,
, 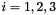 , by linear function
, by linear function 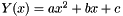 . Returns the coefficients
. Returns the coefficients 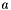 ,
, 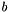 ,
, 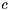 and the error signal 'ser'. For 3 points the minmax fit is computed more quicly compared to the least square fit
and the error signal 'ser'. For 3 points the minmax fit is computed more quicly compared to the least square fit
| [out] | a | The returned coefficients of the interpolating polynomial |
| [out] | b | The returned coefficients of the interpolating polynomial |
| [out] | c | The returned coefficients of the interpolating polynomial |
Definition at line 162 of file RFOF_SpecialSolver.F90.
| subroutine RFOF_SpecialSolver::RFOF_exact_solution | ( | real(8), intent(in) | lambda, |
| real(8), intent(in) | x_in, | ||
| real(8), intent(in) | delta_t, | ||
| real(8), intent(in) | W, | ||
| real(8), intent(in) | A, | ||
| real(8), intent(in) | B, | ||
| real(8), intent(out) | x_fin, | ||
| integer, intent(out) | ser | ||
| ) |
Try to detect anomaly.
Exact solution of the ITO stochastic differential equation 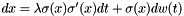 or equivalently
or equivalently 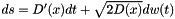 with
with ![$D(x)=[\sigma(x)]^2$](form_90.png) , in the particular case when
, in the particular case when 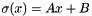 . In the our generic case
. In the our generic case 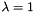 . On the boundary layer
. On the boundary layer 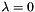 In the case of Stratonovich SDE (not useed here)
In the case of Stratonovich SDE (not useed here) 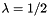
Definition at line 195 of file RFOF_SpecialSolver.F90.
| subroutine RFOF_SpecialSolver::reflect | ( | real(8), intent(in) | miror, |
| real(8), intent(inout) | object_image | ||
| ) |
The exponent must be infinitesimal.
The movement near singular point x=0 is approximated by reflection around cut-of point x_min=miror
Definition at line 219 of file RFOF_SpecialSolver.F90.
| subroutine RFOF_SpecialSolver::RFOF_one_step_generalcase | ( | integer, intent(in) | method, |
| real(8), intent(in) | x_min, | ||
| real(8), intent(in) | delta_t_in, | ||
| real(8), intent(in) | x_in, | ||
| real(8), intent(in) | tolerance, | ||
| real(8), intent(out) | delta_t_out, | ||
| real(8), intent(out) | x_fin, | ||
| real(8), intent(out) | output_error, | ||
| integer, intent(out) | ser | ||
| ) |
Object/image position.
One step solution of the SDE $dx(t)=(x)* d(x)/dx* dt=(x)*dw$ Where $(x)^{2}/2=D(x)=Diffusion_Coefficient(x)$ The algorithm is new, it is based on the local linear approximation: $(x)=Ax+B$ and uses the exact solution
Generate one step RFOF kick, a stochastic difusion , motion from the time delta_t. It is supposed that x_in is in general position, outside of the neighborhood of x=0
| [in] | x_min | If method=1 the robust, strong order 0.5 method is used, recomended near extreme values of x When method=2 , then the strong order 1.5 method is used. |
| [in] | x_min | If method=1 the robust, strong order 0.5 method is used, recomended near extreme values of x When method=2 , then the strong order 1.5 method is used. |
| [in] | delta_t_in | to the value x(t)=x_min, to avoid the singularity at x=0. |
| [in] | x_in | to the value x(t)=x_min, to avoid the singularity at x=0. |
| [out] | x_fin | The allowed relative error |
| [out] | ser | Coefficients of the linear approximation, W is the N(0,1) random number, here lambda=1 |
Definition at line 236 of file RFOF_SpecialSolver.F90.
| subroutine RFOF_SpecialSolver::RFOF_SDE_integrator_corection | ( | real(8), intent(in) | x_min, |
| real(8), intent(in) | x_in, | ||
| real(8), intent(in) | delta_x, | ||
| real(8), dimension(3), intent(in) | sigma, | ||
| real(8), intent(in) | dt, | ||
| real(8), intent(out) | x_final, | ||
| integer | ser | ||
| ) |
Not probable, but be sure.
We are too close to the boundary, the time step will be reduced In this main loop the time step is decreased such that the relative error is less then the input value of "tolerance" sigma**2/2=Diffusion coefficient The correct time step is established. Now we perform 1step , using linear fit and exact solution of the linear SDE, that approximates locally the non-linear SDE W is N(0,1) random number Now the corection that uses the full information on diffusion coefficient, is added We use instead of linear interpolation a quadratic one Higher order, ( strong 1.5 ) correction to result x_final, from subroutine RFOF_one_step_generalcase The full information on the diffusion coefficient is used The algorithm is from: P.E. Kloeden, E. Platten, "Numerical solution of stochastic differential equations", page 351, eq. 4.1 In our use the strong order is 1.5, we have an estimation of reltive error of the order 1 terms
Definition at line 400 of file RFOF_SpecialSolver.F90.
| subroutine RFOF_SpecialSolver::RFOF_multi_step_generalcase | ( | integer, intent(in) | method, |
| real(8), intent(in) | x_min, | ||
| real(8), intent(in) | delta_t_in, | ||
| real(8), intent(out) | delta_t_out, | ||
| real(8), intent(in) | x_in, | ||
| real(8), intent(out) | x_fin, | ||
| real(8), intent(in) | time_in, | ||
| real(8), intent(out) | time_fin, | ||
| real(8), intent(in) | T_max, | ||
| real(8), intent(in) | tolerance, | ||
| ser | |||
| ) |
We use the approximation $(x)=(DiffCoef(x)=mx^2+nx+p)$.
Subroutine for the general case, multistep Multi step solution of the SDE $dx(t)=(x)* d(x)/dx* dt=(x)*dw$ Where $(x)^{2}/2=D(x)=Diffusion_Coefficient(x)$
| [in] | x_min | The method used in one step integration method=1 => use of 0.5 strong order method method=2 => use of 1.5 strong order method |
| [in] | x_min | The method used in one step integration method=1 => use of 0.5 strong order method method=2 => use of 1.5 strong order method |
| [in] | delta_t_in | to the value x(t)=x_min, to avoid the singularity at x=0. |
| [in] | x_in | to the value x(t)=x_min, to avoid the singularity at x=0. |
| [out] | x_fin | The allowed, imposed relative error |
| [in] | time_in | The new position |
| [in] | T_max | The new position |
| [out] | time_fin | The initial time, T_max is the allowend maximal time, |
| [out] | delta_t_out | We have: time_in<time_fin<T_max; The time when the particle leave the boundary domain. t_fin is the time when the movement is stopped due to some event, like too close to singularity ( in this version is not used) |
Definition at line 446 of file RFOF_SpecialSolver.F90.
| subroutine RFOF_SpecialSolver::RFOF_boundary_ymin | ( | real(8), intent(in) | d_prime, |
| real(8), intent(out) | y_min | ||
| ) |
Approximation, works because the singularity of stationary PDF is logarithmic.
Test if exits from the allowed domain y(t)>y_min Increase the time step when it is too small, for a given accuracy end of main time loop
| [in] | d_prime | Compute the minimal value in the regularized variable y: related to x by $x=d'^2 (-2y)$ when 0<x<linearity_approx_limit |
| [out] | y_min | constant, related to the linear aproximation of the diffusion coefficient $D(x)=d'^2/2 xd$ |
Definition at line 605 of file RFOF_SpecialSolver.F90.
| subroutine RFOF_SpecialSolver::RFOF_multi_step_boundarycase | ( | real(8), intent(in) | y_min, |
| real(8), intent(in) | y_max, | ||
| real(8), intent(in) | delta_t_in, | ||
| real(8), intent(in) | y_in, | ||
| real(8), intent(in) | time_in, | ||
| real(8), intent(in) | T_max, | ||
| real(8), intent(in) | tolerance, | ||
| real(8), intent(out) | delta_t_out, | ||
| real(8), intent(out) | y_fin, | ||
| real(8), intent(out) | time_fin, | ||
| integer, intent(out) | ser | ||
| ) |
Solution of the ITO SDE $dy=-0.5(y) dw(t)$ in the domain $0<x<lin_apprx_lim$ or $y>(lin_apprx_lim)/2-(d')=y_{min}$ The variables x and y are related by $x=d'^{2}(-2y)$. The constant d' is defined by the linear approximation of the diffusion coefficient D(x) for 0<x<linearity_approx_limit: $D(x)=d'^2*x/2$ The logarithmic singularity in the x variable at x=0 is regularized. The asymptotic form of the stationary distibution function in new variable y is $(y)=y(-2y)$ The initial value of the time t is t_in, the initial value of the y(t) is y_in The trajectory y(t) is computed while the time (with initial value t_in) is less then T_max, and y(t)<logarithm of the linearity_approx_limit. The time step is adapted such that the relative error is less then the input relative error, denoted "tolerance".
| [in] | y_max | The minimal value of variable y in the SDE $dy=(y)dw(t)/2$ When y<y_min the linear approx breaks and the subroutine returns the variable time_fin Internal variable, the main loop exit when y_curent<y_min |
| [in] | delta_t_in | If the updated value has y(t)>y_max, it is reset to y(t)=y_max, in order to avoid oveflow |
| [in] | y_in | If the updated value has y(t)>y_max, it is reset to y(t)=y_max, in order to avoid oveflow |
| [in] | time_in | initial time step, initial value of variable y |
| [in] | T_max | initial time step, initial value of variable y |
| [out] | time_fin | The the time when the marker enters in the boundary domain; the maximal alowed time |
| [in] | tolerance | The time when the particle leave the boundary domain. time_fin<T_max |
| [out] | delta_t_out | The allowed relative error |
| [out] | y_fin | The allowed relative error |
Definition at line 636 of file RFOF_SpecialSolver.F90.
| subroutine RFOF_SpecialSolver::RFOF_one_step_boundarycase | ( | real(8), intent(in) | y_max, |
| real(8), intent(in) | delta_t, | ||
| real(8), dimension(2), intent(in) | normal_vector, | ||
| real(8), intent(in) | y_in, | ||
| real(8), intent(out) | y_fin, | ||
| real(8), dimension (absolute error for y, relative error for x), intent(out) | error | ||
| ) |
The time step delta_t si decreased at most by a factor 2**maxdivision.
Normal return Main time loop Adjusting the time step to reach exactly the final value T_max, when time_curent is close to T_max The random numbers normal_vector(1), normal_vector(2) will be reused with different time step Internal loop, for adjusting the time step according to given tolerance The counting of time step halving is reseted end time step adjusting loop Test if exits from the allowed domain y(t)>y_min Increase the time step when it is too small, for a given accuracy end of main time loop One-step solver for the SDE, in the boundary region near x=0, or y_min<y<y_max $dy(t)=-0.5 (y)dw(t)$ The algorithm is from: P.E. Kloeden, E. Platten, "Numerical solution of stochastic differential equations", page 351, eq. 4.1 In our use the strong order is 1.5, we have an estimation of relative error of the order 1 terms
| [in] | normal_vector | Esential cut-off parameter If the updated value has y(t)>y_max, it is reset to y(t)=y_max, in order to avoid oveflow |
Definition at line 776 of file RFOF_SpecialSolver.F90.
| real(8) function RFOF_SpecialSolver::exact_moments | ( | real(8), intent(in) | x | ) |
Subroutines for testing.
Computes the exact mean values, in the stationar state: ![$ \mathrm{exact}\_\mathrm{moments}(k)=E_{y}[exp(-ky)] $](form_58.png) For the SDE
For the SDE 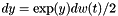
Definition at line 836 of file RFOF_SpecialSolver.F90.
| subroutine RFOF_SpecialSolver::multi_step_boundarytest1 | ( | real(8), intent(in) | ntraject | ) |
Definition at line 845 of file RFOF_SpecialSolver.F90.
| subroutine RFOF_SpecialSolver::boundarytest1_Euler | ( | real(8), intent(in) | y_min, |
| real(8), intent(in) | y_max, | ||
| real(8), intent(in) | y_in, | ||
| real(8), intent(out) | y_fin, | ||
| real(8), intent(in) | t_in, | ||
| real(8), intent(in) | t_fin, | ||
| real(8), intent(in) | ndivision, | ||
| logical, intent(out) | escape | ||
| ) |
End of main loop.
Simple Euler-Maruyana solver for the SDE
![\[ dy(t)=-0.5 \exp(y)dw(t) \]](form_135.png)
| [in] | y_min | The lowest limit of the allowed domain If 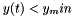 the subroutine stops the subroutine stops |
| [in] | y_max | If the updated value has y(t)>y_max, it is reset to 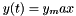 , in order to avoid overflow , in order to avoid overflow |
| [in] | y_in | initial position |
| [in] | t_in | start time |
| [in] | t_fin | final time |
| [in] | ndivision | Number of discretisation of the time interval |
| [out] | y_fin | final position |
| [out] | escape | True if 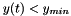 for some for some 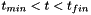 |
Definition at line 987 of file RFOF_SpecialSolver.F90.
| subroutine RFOF_SpecialSolver::multi_step_generaltest3 | ( | real(8), intent(in) | ntraject | ) |
Test the solver for the SDE 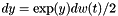 , by computing mean values in stationary state and comparing with the exact values given by simpest Euler method Test of subroutine RFOF_multi_step_boundarycase for
, by computing mean values in stationary state and comparing with the exact values given by simpest Euler method Test of subroutine RFOF_multi_step_boundarycase for 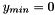 .
.
| [in] | ntraject | Number of trajectories in MC sampling |
Definition at line 1059 of file RFOF_SpecialSolver.F90.
| subroutine RFOF_SpecialSolver::generaltest3_Euler | ( | real(8), intent(in) | x_min, |
| real(8), intent(in) | x_in, | ||
| real(8), intent(out) | x_fin, | ||
| real(8), intent(in) | t_in, | ||
| real(8), intent(in) | t_fin, | ||
| real(8), intent(in) | ndivision, | ||
| integer | ser | ||
| ) |
Simple Euler-Maruyana solver for the SDE 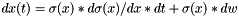 where
where 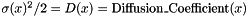 .
.
| [in] | x_in | If x(t)<x_min the subroutine stops then approximate: 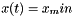 , in order to avoid singular behavior , in order to avoid singular behavior |
| ser | The derivative is used only for the test of subroutine |
Definition at line 1230 of file RFOF_SpecialSolver.F90.