RFOF - RF Library for Orbit Following Codes
Data Types | Public Member Functions
RFOF_kick Module Reference

Module handling wave acceleartion physics, i.e. the Monte Carlo kicks. More...

List of all members.

Data Types

type  coeff_for_guiding_centre_kick
 Coefficients defining the direction of the RF acceleration (for a single mode) in the configuration space 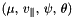$(\mu, \, v_\|, \, \psi, \, \theta)$. More...

Public Member Functions

subroutine quasilinear_RF_kick_steinbrecher_integrator (marker, mem, Blocal, RFlocal, RFglobal, diagno, MPI_node_Id)
 Quasilinear RF Monte Carlo kicks for time-accelerated orbit following as described in [Eriksson, Phys. Plasmas 12, 072524 (2005)].

Detailed Description

Module handling wave acceleartion physics, i.e. the Monte Carlo kicks.

At present there are three types of Monte Carlo-kick-opertors:

  • quasilinear_RF_kick_steinbrecher_integrator an advanced operator still under development
  • quasilinear_RF_kick_with_time_acceleration one simpler form which can only treat single crossings of the resonance
  • RFkick_single_pass and one more advanced one which can account for time-accelerated orbit tracing in which each crossing of the resonance corresponds to a number NACC real crossing. This the theory for treating the time-accelerated case is described in [L.-G. Eriksson and M. Schneider, Phys. Plasmas 12, 072524 (2005), http://pop.aip.org/resource/1/phpaen/v12/i7/p072524_s1 ].
Author:
T. Johnson
Date:
2010.08.28
Version:
"$Id: RFOF_kick.F90 211 2011-09-26 16:48:30Z tjohnson $"

Definition at line 23 of file RFOF_kick.F90.

Member Function/Subroutine Documentation

subroutine RFOF_kick::quasilinear_RF_kick_steinbrecher_integrator ( type(particle), intent(inout), target  marker,
type(resonance_memory), intent(in), target  mem,
type(magnetic_field_local), intent(inout), target  Blocal,
type(rf_wave_local), intent(inout), target  RFlocal,
type(rf_wave_global), intent(in), target  RFglobal,
type(RFOF_cumlative_diagnostics), intent(inout)  diagno,
integer, intent(in)  MPI_node_Id 
)

Quasilinear RF Monte Carlo kicks for time-accelerated orbit following as described in [Eriksson, Phys. Plasmas 12, 072524 (2005)].

Attention:
dIperp and drift is in units [MeV], while diffusion is in [(MeV)^2]. These untis (cmp. SI units) give less truncation errors in the numerical derivative performed in performed to calculate drift.
Todo:

Improve the Monte Carlo stepping scheme to something adaptive. Introduce a check to see that the RF step has given a physical orbit.

What to do with the diffusion and drift coefficients going into the diagnostics?

INPUT

Parameters:
mem(in) Short term memory of the resonance condition along the orbit
RFglobal(in) Global properties of the RF wave field
MPI_node_Id(in) Number used to identify MPI nods during parallel execusion.

INPUT/OUTPUT

Parameters:
marker(inout) Properties of the marker
Blocal(inout) Local properties of the magnetic field
RFlocal(inout) Local properties of the RF wave field
diagno(inout) Time cumulative diagnostics (to be updated as marker is accelerated by the RF wave field)

Definition at line 81 of file RFOF_kick.F90.

References MC_kick_steinbrecher_integrator(), wrap_move_marker_on_characteristic(), and wrap_RF_diffusion_and_move_marker().

+ Here is the call graph for this function:

The documentation for this module was generated from the following file: