 |
RFOF - RF Library for Orbit Following Codes
|
 |
RFOF - RF Library for Orbit Following Codes
|
In RFOF_SpecialSolver5.f90 the regularization method 1 means reflection at X_MIN and X_MAX, the boundaries of the allowed domain. Contains subroutines for solution of one dimesional stochastic differential equation for Monte-Carlo simulation of RF heating:
![\[ dx(t)=D'(x)dt+\sqrt(2 D(x)) dw(t) \]](form_107.png)
In this version we use a combination of 2 integration methods. Both integration methods use 3 kind of treating of the singularity at x=0,called regularization methods. Regularization method 0 means no regularization The test is performed by comparing the result with a simplest Euler method in the case of an artificial form of the diffusion coefficient. These methods are addaptive: the time step size is modified according to a prescribed relative tolerance In this version the program is stopped, with suitable error message, in the case when the required relative error cannot be attained in a resonable time Two integration methods are used. The input is the the function 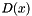 , the diffusion coefficient. The function
, the diffusion coefficient. The function 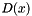 is computed in 3 points.The 3 points are selected such that the best linear approximation of
is computed in 3 points.The 3 points are selected such that the best linear approximation of
![\[ \sigma(x)=\sqrt(2 D(x))\]](form_110.png)
, has a relative tolerance less then a given input relative error In both integration methods a local linear approximation of 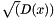 , according to given input relative tollerance is generated. In the method 1 the exact solution of the approximate linear equation is used for update, we have a strong 1/2 order method This method is usefull near
, according to given input relative tollerance is generated. In the method 1 the exact solution of the approximate linear equation is used for update, we have a strong 1/2 order method This method is usefull near 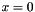 , no assumptions are made on higer order derivatives. In the integration method 2 an extrapolation is performed, by using the same information on
, no assumptions are made on higer order derivatives. In the integration method 2 an extrapolation is performed, by using the same information on 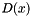 : a quadratic approximation of
: a quadratic approximation of 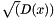 is generated an from this approximation the analytic form of the derivatives of the terms of SDE are generated, that are used to generate a strong 3/2 order stochastic integrator. This is recomended to use for larger values of x. The main problem is the that near
is generated an from this approximation the analytic form of the derivatives of the terms of SDE are generated, that are used to generate a strong 3/2 order stochastic integrator. This is recomended to use for larger values of x. The main problem is the that near 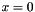 the term
the term 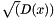 is not differentiable, so a regularization is needed. Two regularization methods are used, for both integration methods, method 1 and method 2. In the our notatation regularization method 0 means no regularization. In the regularization method 1 when
is not differentiable, so a regularization is needed. Two regularization methods are used, for both integration methods, method 1 and method 2. In the our notatation regularization method 0 means no regularization. In the regularization method 1 when 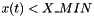 or
or 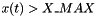 , then
, then 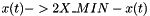 , or
, or 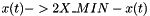 (subroutine Correction_domain_boundary ). Method 2 use an input small parameter,reg_param_diff_coef, that is small compared to the typical mean value of the diffusion coefficient ( see below) . In the regularization method 2, the behavior near x=0 , is modified: the function
(subroutine Correction_domain_boundary ). Method 2 use an input small parameter,reg_param_diff_coef, that is small compared to the typical mean value of the diffusion coefficient ( see below) . In the regularization method 2, the behavior near x=0 , is modified: the function 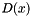 is replaced by
is replaced by
![\[ \sqrt( D(x)^2+reg\_param\_diff\_coef^2)\]](form_142.png)
The parameter reg_param_diff_coef is defined in the term of the input parameter mean_diff_coef, that is an estimate of the typical order of magnitude of the diffusion coefficient, and the parameter small_adimensional_diff_coef_fact that can be chosen related to the imposed relative Monte-Carlo tolerance. TO DO: Computation of the cutoff parameters 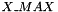 ,
, 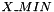 introduced, in order to define the allowed domain of motion. call diffusion_coefficient4(x,diff_coeficient,Error_flag), used for test, to be replaced by RFOF module.
More...
introduced, in order to define the allowed domain of motion. call diffusion_coefficient4(x,diff_coeficient,Error_flag), used for test, to be replaced by RFOF module.
More...
Public Member Functions | |
| subroutine | correction_domain_boundary (X_inout) |
subroutine correction_domain_boundary(X_inout ) When X_inout is outside of the domain 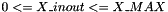 , it is put inside by reflection on the boundaries , it is put inside by reflection on the boundaries | |
| logical function | aprox_equal (x, y) |
| function aprox_equal(x,y) result(yes_no) | |
| subroutine | RFOF_regularized_diffusion_coef (diff_coef, regularization_method, regularized_diff_coef) |
Regularizations designed to replace the x->0 behavior 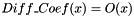 by by 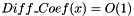 for method 2, respectively the movement is stopped in the. for method 2, respectively the movement is stopped in the. | |
| subroutine | RFOF_regularized_diffusion_coef_Euler (x, regularization_method, regularized_diff_coef, derivative_reg_diff_coef, Error_Flag) |
Version of the previous subroutine. It is used only in test runs, when it is called by the reference Euler subroutine. It returns also the regularized derivative Regularization designed to replace the 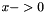 behavior behavior 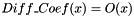 by by 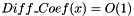 for method 2 For for method 2 For 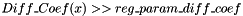 we have asymptotice equality for method 2. we have asymptotice equality for method 2. | |
| subroutine | RFOF_sigma (regularization_method, x, sigma, Error_flag) |
| The relation to the diffusion coefficient is:
When regularization_method=0, no regularization. In the regularization method 2, the behavior near x=0 , is modified: the function
when regularization_method=1 is used, when the trajectory steps outside the allowed domain, it is reflected | |
| subroutine | linear_fit (x, y, A, B, Error_Flag) |
| Linear fit : y(i)=A*x(i)+B; i=1,2. Returns the coefficients. | |
| subroutine | linear_aprox_minmax (x, y, A, B, minmaxerr, Error_Flag) |
| Find the best min-max approximation of the 3 points with coordinates
by linear function
. Returns the coefficients A,B and the relative error and the error signal. For 3 points the minmax fit is computed more quicly compared to the least square fit. | |
| subroutine | linear_aprox_minmax2 (xc, delta, y, A, B, minmaxerr, Error_Flag) |
| The same as the previous subroutine linear_aprox_minmax, but in this case the x points are equidistants Their coordinates are: x(1)=x(2)-delta; x(3)=x(2)+delta; We denoted:x(2)=xc Find the best min-max approximation of the 3 points with coordinates [x(i), y(i)], i=1,2,3, by linear function y(x)=Ax+B.Returns the coefficients A,B and the relative error and the error signal. For 3 points the minmax fit is computed more quicly compared to the least square fit. | |
| subroutine | quadratic_interpolation (xc, delta_x, y, a, b, c, Error_Flag) |
| Quadratic interpolation Y(x)=ax^2+bx+c of the values of the array y(3) in the x points, given by the array x(3), where the points x(1), x(2), x(3) that are equidistants Their coordinates are: x(1)=x(2)-delta; x(3)=x(2)+delta; We denoted the centrak point:x(2)=xc Find the polinomial interpolation of the 3 points with coordinates [x(i), y(i)], i=1,2,3, by linear function Y(x)=ax^2+bx+c .Returns the coefficients a, b, c and the error signal 'Error_Flag'. For 3 points the minmax fit is computed more quicly compared to the least square fit. | |
| subroutine | RFOF_exact_solution (lambda, x_in, delta_t, W, A, B, x_fin, Error_Flag) |
| Exact solution of the ITO stochastic differential equation $dx= (x) '(x) dt +(x) dw(t)$ or equivalently $ds=D'(x)dt+{2D(x)}dw(t)$ with $D(x)=[(x)]^2$, in the particular case when $(x)=Ax+B$. In the our generic case $=1$. On the boundary layer $lambda=0$ In the case of Stratonovich SDE (not useed here) $=1/2$. | |
| subroutine | reflect (mirror, object_image) |
| The movement near singular point x=0 is approximated by reflection around cut-of point x_min=mirror. | |
| subroutine | RFOF_one_step_generalcase (integration_method, regularization_method, delta_t_in, x_in, tolerance, delta_t_out, x_fin, output_error, nr_subdivision, Error_Flag) |
| subroutine RFOF_one_step_generalcase(integration_method,regularization_method,delta_t_in,& x_in, tolerance,delta_t_out,x_fin, output_error,nr_subdivision ,Error_Flag) One step solution of the SDE $dx(t)=(x)* d(x)/dx* dt=(x)*dw$ Where $(x)^{2}/2=D(x)=Diffusion_Coefficient(x)$ The algorithm is new, it is based on the local linear approximation: $(x)=Ax+B$ and uses the exact solution | |
| subroutine | RFOF_SDE_integrator_corection (xx, sigma, dt, x_final, Error_Flag) |
| W is N(0,1) random number. | |
| subroutine | RFOF_multi_step_generalcase (integration_method, regularization_method, delta_t_in, delta_t_out, x_in, x_fin, time_in, time_fin, T_max, tolerance, Error_Flag) |
Subroutine for the general case, multistep Multi step solution of the SDE 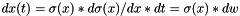 Where Where 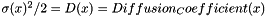 . . | |
Public Attributes | |
| real(8), parameter | mean_diff_coef = 1.d0 |
| real(8), parameter | small_adimensional_diff_coef_fact = 1.0d-3 |
| TO DO: link to RFOF modules and compute automatically Typical value, given at least as order of magnitude of the diffusion coefficient. | |
| real(8), parameter | reg_param_diff_coef = mean_diff_coef*small_adimensional_diff_coef_fact |
| Used in Regularization method 1 and Adimensional small number, defines the accuracy of the approximation of the diffusion coefficient near zero value of the magnetic momentum. | |
| real(8), parameter | reg_param_diff_coef2 = reg_param_diff_coef*reg_param_diff_coef |
| real(8), parameter | X_MIN = 1.0d-3 |
| real(8), parameter | X_MAX = 1.0d4 * X_MIN |
| Recommended:order of magn(X_MIN)=small_adimensional_parameter**2*q**2/mass* <B/k_perp**2 > | |
In RFOF_SpecialSolver5.f90 the regularization method 1 means reflection at X_MIN and X_MAX, the boundaries of the allowed domain. Contains subroutines for solution of one dimesional stochastic differential equation for Monte-Carlo simulation of RF heating:
![\[ dx(t)=D'(x)dt+\sqrt(2 D(x)) dw(t) \]](form_107.png)
In this version we use a combination of 2 integration methods. Both integration methods use 3 kind of treating of the singularity at x=0,called regularization methods. Regularization method 0 means no regularization The test is performed by comparing the result with a simplest Euler method in the case of an artificial form of the diffusion coefficient. These methods are addaptive: the time step size is modified according to a prescribed relative tolerance In this version the program is stopped, with suitable error message, in the case when the required relative error cannot be attained in a resonable time Two integration methods are used. The input is the the function 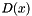 , the diffusion coefficient. The function
, the diffusion coefficient. The function 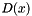 is computed in 3 points.The 3 points are selected such that the best linear approximation of
is computed in 3 points.The 3 points are selected such that the best linear approximation of
![\[ \sigma(x)=\sqrt(2 D(x))\]](form_110.png)
, has a relative tolerance less then a given input relative error In both integration methods a local linear approximation of 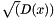 , according to given input relative tollerance is generated. In the method 1 the exact solution of the approximate linear equation is used for update, we have a strong 1/2 order method This method is usefull near
, according to given input relative tollerance is generated. In the method 1 the exact solution of the approximate linear equation is used for update, we have a strong 1/2 order method This method is usefull near 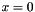 , no assumptions are made on higer order derivatives. In the integration method 2 an extrapolation is performed, by using the same information on
, no assumptions are made on higer order derivatives. In the integration method 2 an extrapolation is performed, by using the same information on 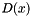 : a quadratic approximation of
: a quadratic approximation of 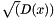 is generated an from this approximation the analytic form of the derivatives of the terms of SDE are generated, that are used to generate a strong 3/2 order stochastic integrator. This is recomended to use for larger values of x. The main problem is the that near
is generated an from this approximation the analytic form of the derivatives of the terms of SDE are generated, that are used to generate a strong 3/2 order stochastic integrator. This is recomended to use for larger values of x. The main problem is the that near 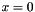 the term
the term 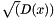 is not differentiable, so a regularization is needed. Two regularization methods are used, for both integration methods, method 1 and method 2. In the our notatation regularization method 0 means no regularization. In the regularization method 1 when
is not differentiable, so a regularization is needed. Two regularization methods are used, for both integration methods, method 1 and method 2. In the our notatation regularization method 0 means no regularization. In the regularization method 1 when 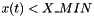 or
or 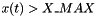 , then
, then 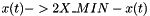 , or
, or 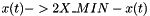 (subroutine Correction_domain_boundary ). Method 2 use an input small parameter,reg_param_diff_coef, that is small compared to the typical mean value of the diffusion coefficient ( see below) . In the regularization method 2, the behavior near x=0 , is modified: the function
(subroutine Correction_domain_boundary ). Method 2 use an input small parameter,reg_param_diff_coef, that is small compared to the typical mean value of the diffusion coefficient ( see below) . In the regularization method 2, the behavior near x=0 , is modified: the function 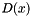 is replaced by
is replaced by
![\[ \sqrt( D(x)^2+reg\_param\_diff\_coef^2)\]](form_142.png)
The parameter reg_param_diff_coef is defined in the term of the input parameter mean_diff_coef, that is an estimate of the typical order of magnitude of the diffusion coefficient, and the parameter small_adimensional_diff_coef_fact that can be chosen related to the imposed relative Monte-Carlo tolerance. TO DO: Computation of the cutoff parameters 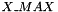 ,
, 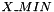 introduced, in order to define the allowed domain of motion. call diffusion_coefficient4(x,diff_coeficient,Error_flag), used for test, to be replaced by RFOF module.
introduced, in order to define the allowed domain of motion. call diffusion_coefficient4(x,diff_coeficient,Error_flag), used for test, to be replaced by RFOF module.
Definition at line 56 of file RFOF_SpecialSolver5.F90.
| subroutine RFOF_SpecialSolver5::correction_domain_boundary | ( | real(8), intent(inout) | X_inout | ) |
subroutine correction_domain_boundary(X_inout ) When X_inout is outside of the domain 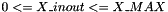 , it is put inside by reflection on the boundaries
, it is put inside by reflection on the boundaries
Definition at line 93 of file RFOF_SpecialSolver5.F90.
| logical function RFOF_SpecialSolver5::aprox_equal | ( | real(8), intent(in) | x, |
| real(8), intent(in) | y | ||
| ) |
function aprox_equal(x,y) result(yes_no)
Return true if the relative error of x,y is less then the internal eror. CAUTION: Must be used ONLYin situations when the aproximate equality of x=y must be detected, x, y perturbed by round-off errors AND neither x=0 or y=0 occur, like in the subroutines below, where the actual relative error is generated by floating point round-off
Definition at line 116 of file RFOF_SpecialSolver5.F90.
| subroutine RFOF_SpecialSolver5::RFOF_regularized_diffusion_coef | ( | real(8), intent(in) | diff_coef, |
| integer, intent(in) | regularization_method, | ||
| real(8), intent(out) | regularized_diff_coef | ||
| ) |
Regularizations designed to replace the x->0 behavior 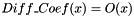 by
by 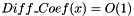 for method 2, respectively the movement is stopped in the.
for method 2, respectively the movement is stopped in the.
For 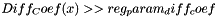 we have asymptotic equality for both methods
we have asymptotic equality for both methods
Definition at line 139 of file RFOF_SpecialSolver5.F90.
| subroutine RFOF_SpecialSolver5::RFOF_regularized_diffusion_coef_Euler | ( | real(8), intent(in) | x, |
| integer, intent(in) | regularization_method, | ||
| real(8), intent(out) | regularized_diff_coef, | ||
| real(8), intent(out) | derivative_reg_diff_coef, | ||
| integer, intent(out) | Error_Flag | ||
| ) |
Version of the previous subroutine. It is used only in test runs, when it is called by the reference Euler subroutine. It returns also the regularized derivative Regularization designed to replace the 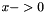 behavior
behavior 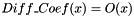 by
by 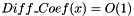 for method 2 For
for method 2 For 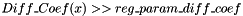 we have asymptotice equality for method 2.
we have asymptotice equality for method 2.
Definition at line 167 of file RFOF_SpecialSolver5.F90.
| subroutine RFOF_SpecialSolver5::RFOF_sigma | ( | integer, intent(in) | regularization_method, |
| real(8), intent(in) | x, | ||
| real(8), intent(out) | sigma, | ||
| integer, intent(out) | Error_flag | ||
| ) |
The relation to the diffusion coefficient is:
![\[ (RFOF\_sigma(x))^2=diffusion\_coefficient(x) \]](form_150.png)
When regularization_method=0, no regularization. In the regularization method 2, the behavior near x=0 , is modified: the function 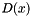 is replaced by
is replaced by
![\[ \sqrt( D(x)^2+reg\_param\_diff\_coef^2 ) \]](form_151.png)
when regularization_method=1 is used, when the trajectory steps outside the allowed domain, it is reflected 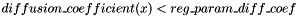 , an small parameter The parameter is
, an small parameter The parameter is 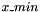 .
.
Definition at line 217 of file RFOF_SpecialSolver5.F90.
| subroutine RFOF_SpecialSolver5::linear_fit | ( | real(8), dimension(2), intent(in) | x, |
| real(8), dimension(2), intent(in) | y, | ||
| real(8), intent(out) | A, | ||
| real(8), intent(out) | B, | ||
| integer, intent(out) | Error_Flag | ||
| ) |
Linear fit : y(i)=A*x(i)+B; i=1,2. Returns the coefficients.
Definition at line 261 of file RFOF_SpecialSolver5.F90.
| subroutine RFOF_SpecialSolver5::linear_aprox_minmax | ( | real(8), dimension(3), intent(in) | x, |
| real(8), dimension(3), intent(in) | y, | ||
| real(8), intent(out) | A, | ||
| real(8), intent(out) | B, | ||
| real(8), intent(out) | minmaxerr, | ||
| integer, intent(out) | Error_Flag | ||
| ) |
Find the best min-max approximation of the 3 points with coordinates
![\[ [x(i), y(i)], i=1,2,3, \]](form_154.png)
by linear function
![\[ y(x)=Ax+B \]](form_155.png)
. Returns the coefficients A,B and the relative error and the error signal. For 3 points the minmax fit is computed more quicly compared to the least square fit.
Definition at line 286 of file RFOF_SpecialSolver5.F90.
| subroutine RFOF_SpecialSolver5::linear_aprox_minmax2 | ( | real(8), intent(in) | xc, |
| real(8), intent(in) | delta, | ||
| real(8), dimension(3), intent(in) | y, | ||
| real(8), intent(out) | A, | ||
| real(8), intent(out) | B, | ||
| real(8), intent(out) | minmaxerr, | ||
| integer, intent(out) | Error_Flag | ||
| ) |
The same as the previous subroutine linear_aprox_minmax, but in this case the x points are equidistants Their coordinates are: x(1)=x(2)-delta; x(3)=x(2)+delta; We denoted:x(2)=xc Find the best min-max approximation of the 3 points with coordinates [x(i), y(i)], i=1,2,3, by linear function y(x)=Ax+B.Returns the coefficients A,B and the relative error and the error signal. For 3 points the minmax fit is computed more quicly compared to the least square fit.
Definition at line 322 of file RFOF_SpecialSolver5.F90.
| subroutine RFOF_SpecialSolver5::quadratic_interpolation | ( | real(8), intent(in) | xc, |
| real(8), intent(in) | delta_x, | ||
| real(8), dimension(3), intent(in) | y, | ||
| real(8), intent(out) | a, | ||
| real(8), intent(out) | b, | ||
| real(8), intent(out) | c, | ||
| integer, intent(out) | Error_Flag | ||
| ) |
Quadratic interpolation Y(x)=ax^2+bx+c of the values of the array y(3) in the x points, given by the array x(3), where the points x(1), x(2), x(3) that are equidistants Their coordinates are: x(1)=x(2)-delta; x(3)=x(2)+delta; We denoted the centrak point:x(2)=xc Find the polinomial interpolation of the 3 points with coordinates [x(i), y(i)], i=1,2,3, by linear function Y(x)=ax^2+bx+c .Returns the coefficients a, b, c and the error signal 'Error_Flag'. For 3 points the minmax fit is computed more quicly compared to the least square fit.
Definition at line 359 of file RFOF_SpecialSolver5.F90.
| subroutine RFOF_SpecialSolver5::RFOF_exact_solution | ( | real(8), intent(in) | lambda, |
| real(8), intent(in) | x_in, | ||
| real(8), intent(in) | delta_t, | ||
| real(8), intent(in) | W, | ||
| real(8), intent(in) | A, | ||
| real(8), intent(in) | B, | ||
| real(8), intent(out) | x_fin, | ||
| integer, intent(out) | Error_Flag | ||
| ) |
Exact solution of the ITO stochastic differential equation $dx= (x) '(x) dt +(x) dw(t)$ or equivalently $ds=D'(x)dt+{2D(x)}dw(t)$ with $D(x)=[(x)]^2$, in the particular case when $(x)=Ax+B$. In the our generic case $=1$. On the boundary layer $lambda=0$ In the case of Stratonovich SDE (not useed here) $=1/2$.
Definition at line 392 of file RFOF_SpecialSolver5.F90.
| subroutine RFOF_SpecialSolver5::reflect | ( | real(8), intent(in) | mirror, |
| real(8), intent(inout) | object_image | ||
| ) |
The movement near singular point x=0 is approximated by reflection around cut-of point x_min=mirror.
Definition at line 419 of file RFOF_SpecialSolver5.F90.
| subroutine RFOF_SpecialSolver5::RFOF_one_step_generalcase | ( | integer, intent(in) | integration_method, |
| integer, intent(in) | regularization_method, | ||
| real(8), intent(in) | delta_t_in, | ||
| real(8), intent(in) | x_in, | ||
| real(8), intent(in) | tolerance, | ||
| real(8), intent(out) | delta_t_out, | ||
| real(8), intent(out) | x_fin, | ||
| real(8), intent(out) | output_error, | ||
| integer, intent(out) | nr_subdivision, | ||
| integer, intent(out) | Error_Flag | ||
| ) |
subroutine RFOF_one_step_generalcase(integration_method,regularization_method,delta_t_in,& x_in, tolerance,delta_t_out,x_fin, output_error,nr_subdivision ,Error_Flag) One step solution of the SDE $dx(t)=(x)* d(x)/dx* dt=(x)*dw$ Where $(x)^{2}/2=D(x)=Diffusion_Coefficient(x)$ The algorithm is new, it is based on the local linear approximation: $(x)=Ax+B$ and uses the exact solution
Generate one step RFOF kick, a stochastic difusion , motion from the time delta_t. It is supposed that x_in is in general position, outside of the neighborhood of x=0 The error signal Error_Flag=0 when OK. Error_Flag=1 when by succesive reducing the time step the accuracy is still greater then tolerance Error_Flag=2 when the input initial position is wrong Error_Flag=3 when the input time step is wrong Error_Flag=4 when the input initial time is wrong Error_Flag=7: Too large exponent in the subroutine RFOF_Exact_Solution Error_Flag=8 when the error signal from called subroutine linear_aprox_minmax2 is nonzero Error_Flag=9 Improbable value of the diffusion coefficient Error_Flag=10 when the error signal from called subroutine for diffusion coefficient is nonzero Error_Flag=11, when the normalized magnetic momentum, "x", is negative or zero (x=0 is a sticking point ) Error_Flag=12, when the values of the diffusion coefficient are zero Error_Flag=14 when the integer "smoothing_method" from subroutine RFOF_sigma is not 1 or2 Error_Flag=15 anomalous return to subroutine RFOF_SDE_integrator_corection from the quadratic interpolatin subroutine polycoef_3points, stored in the file RFOF_numerics.f90 (module RFOF_numerics) Error_Flag=16 The initial point is outside the allowed domain, imposed by regularization_method 1 The signal is from subroutine RFOF_multi_step_generalcase
Definition at line 454 of file RFOF_SpecialSolver5.F90.
| subroutine RFOF_SpecialSolver5::RFOF_SDE_integrator_corection | ( | real(8), dimension(3), intent(in) | xx, |
| real(8), dimension(3), intent(in) | sigma, | ||
| real(8), intent(in) | dt, | ||
| real(8), intent(out) | x_final, | ||
| integer | Error_Flag | ||
| ) |
W is N(0,1) random number.
Higher order, ( strong 1.5 ) correction to result x_final, from subroutine RFOF_one_step_generalcase The full information on the diffusion coefficient is used The algorithm is from: P.E. Kloeden, E. Platten, "Numerical solution of stochastic differential equations", page 351, eq. 4.1 In our use the strong order is 1.5, we have an estimation of reltive error of the order 1 terms
Definition at line 610 of file RFOF_SpecialSolver5.F90.
References polycoef_3points().
 Here is the call graph for this function:
Here is the call graph for this function:| subroutine RFOF_SpecialSolver5::RFOF_multi_step_generalcase | ( | integer, intent(in) | integration_method, |
| integer, intent(in) | regularization_method, | ||
| real(8), intent(in) | delta_t_in, | ||
| real(8), intent(out) | delta_t_out, | ||
| real(8), intent(in) | x_in, | ||
| real(8), intent(out) | x_fin, | ||
| real(8), intent(in) | time_in, | ||
| real(8), intent(out) | time_fin, | ||
| real(8), intent(in) | T_max, | ||
| real(8), intent(in) | tolerance, | ||
| integer, intent(out) | Error_Flag | ||
| ) |
Subroutine for the general case, multistep Multi step solution of the SDE 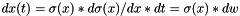 Where
Where 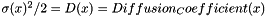 .
.
Definition at line 669 of file RFOF_SpecialSolver5.F90.
| real(8), parameter RFOF_SpecialSolver5::mean_diff_coef = 1.d0 |
Definition at line 65 of file RFOF_SpecialSolver5.F90.
| real(8), parameter RFOF_SpecialSolver5::small_adimensional_diff_coef_fact = 1.0d-3 |
TO DO: link to RFOF modules and compute automatically Typical value, given at least as order of magnitude of the diffusion coefficient.
Definition at line 68 of file RFOF_SpecialSolver5.F90.
| real(8), parameter RFOF_SpecialSolver5::reg_param_diff_coef = mean_diff_coef*small_adimensional_diff_coef_fact |
Used in Regularization method 1 and Adimensional small number, defines the accuracy of the approximation of the diffusion coefficient near zero value of the magnetic momentum.
Definition at line 73 of file RFOF_SpecialSolver5.F90.
| real(8), parameter RFOF_SpecialSolver5::reg_param_diff_coef2 = reg_param_diff_coef*reg_param_diff_coef |
Definition at line 75 of file RFOF_SpecialSolver5.F90.
| real(8), parameter RFOF_SpecialSolver5::X_MIN = 1.0d-3 |
Definition at line 76 of file RFOF_SpecialSolver5.F90.
| real(8), parameter RFOF_SpecialSolver5::X_MAX = 1.0d4 * X_MIN |
Recommended:order of magn(X_MIN)=small_adimensional_parameter**2*q**2/mass* <B/k_perp**2 >
Definition at line 78 of file RFOF_SpecialSolver5.F90.