Running Exponential Average
Overview
In conventional transport modelling, turbulent fluxes are modelled in terms of processes which are diffusive in the local relaxation sense, with the average flux given by a diffusion coefficient and an effective pinch velocity. The equations are of dominantly parabolic character, which means in practice that an iterate will move monotonically towards the solution in parameter space.
This is not the case for turbulence. Convergence is statistical, which is something different than a diffusive relaxation. If turbulence is stationary, it is meant only that the mean of a distribution of iterates is stationary, not the iterates themselves. The standard deviation can be significant, of order unity compared to the mean, of any distribution of iterates.
This makes for a noisy signal if the output of a turbulence code is used for transport coefficients in a workflow. A sound way to overcome the attendant problems is to use a moving average. Even an average over a moving window can be as noisy as the original signal, however. What works better is a weighted average over recent past values. A method to get this is called a running exponential average, which is essentially the same thing as a convolution integral over an exponential memory decay times the past signal. It turns out to be very easy to obtain this without saving past values.
The original reference for the following is S W Roberts, "Control Chart Tests Based on Geometric Moving Averages," Technometrics1 (1959) 239-250, cited by all the good WWW resources, including the Wikipedia page on Moving Averages and the NIST Statistical Handbook online.
Definition
Consider a process 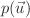 which is a
functional of dependent variables
which is a
functional of dependent variables 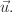 Measure
Measure 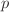 at discrete time intervals
at discrete time intervals
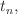 with values
with values 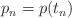 and interval length
and interval length  The moving exponential average
The moving exponential average 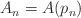 on
the
on
the 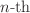 interval is
defined as
interval is
defined as
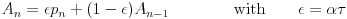
|
 is given in
terms of the interval
is given in
terms of the interval  and an inverse time
constant
and an inverse time
constant 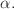
In the first instance 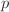 is measured there
is no
is measured there
is no 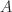 so the first value of
so the first value of
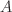 is simply set to
is simply set to 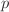 since it can be assumed that the initial state for
since it can be assumed that the initial state for
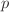 has persisted for infinite previous time up to
the initial time point.
has persisted for infinite previous time up to
the initial time point.
Differential Equation
The equivalent differential equation is found by forming the relevant finite difference,
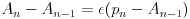
|
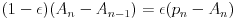
|
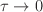 is the same as taking
is the same as taking 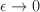 so both
of these expressions become equivalent to
so both
of these expressions become equivalent to
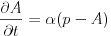
|
Equivalence to Past-Time Convolution Integral
The solution of the above differential equation is given by the method of undetermined coefficients,
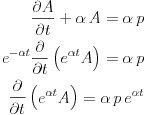
|
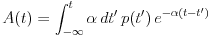
|
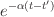 and the signal
and the signal 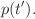 The time constant
The time constant 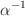 is just the
memory decay time, while if
is just the
memory decay time, while if 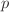 is constant then the integral yields
unity times
is constant then the integral yields
unity times 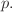 This is the same as the normalisation with the
This is the same as the normalisation with the
 factor in the average formula above, which is needed since
the interval is of finite size.
factor in the average formula above, which is needed since
the interval is of finite size.
Hence the running exponential average is operationally the same as a
memory decay integral over past time. The elegant feature is the need
to keep only the current value of 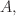 as it
already contains all that is needed of the past time evolution
of
as it
already contains all that is needed of the past time evolution
of 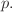
notes
Some properties of the running exponential average and how to choose its main time-memory parameter:
- The
 factor is needed
for normalisation
factor is needed
for normalisation
- if
 then
then
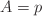 for all
for all 
- the integral with
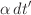 yields unity
yields unity - the
 and
and
 factors add to
unity
factors add to
unity - therefore set the first value of
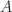 to the first value of
to the first value of
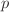
- the integral with
- in choosing the memory decay time
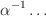
- one should have

- best results are for
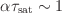
- some trial/error required; edge turbulence likes
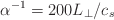
- one should have
In these expressions  and
and
 are the correlation and
saturation times of the turbulence, respectively.
are the correlation and
saturation times of the turbulence, respectively.
last update: 2012-03-19 by bscott
