Turbulent Flux Quantities in Transport Models
Overview
In conventional transport modelling, all quantities appearing in the
equations are 1-D, in some radial coordinate (poloidal flux,
normalised radius, etc). In general any monotonic radial coordinate
is acceptable. In the TF-ITM, the toroidal flux radius is standard.
All we need from the radial coordinate is the transformation to get
to 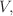 the volume enclosed by the flux surface,
which is fundamental to the governing equations, which are conservation
laws.
the volume enclosed by the flux surface,
which is fundamental to the governing equations, which are conservation
laws.
What we have to do is to take a measured result, which is a time-averaged fluctuation-based transport flux and turn it into 1-D quantities suitable to modelling. This is done using the flux surface average, explained in conventions. The transport equations themselves constitute a mean field approximation to the 3-D conservation laws. For the fundamentals encountered in transport modelling see R Hazeltine and J Meiss, Plasma Confinement (Addison-Wesley, 1992) chapter 8. For the special properties of transport driven by small-scale pressure driven ExB microturbulence see B Scott, "The character of transport caused by ExB drift turbulence," Phys Plasmas 10 (2003) 963-976.
For ambipolarity we follow the rules for dynamical alignment, which follows the physics of how electron fluctuations determine the ExB velocity fluctuations, which then advect all species. Magnetic flutter nonlinearities act independently of this, but in our modelling they are used solely for heat fluxes since the averaged particle transport due to magnetic flutter and the current cancels, leaving the parallel ion velocity which we neglect for this purpose. The reference for dynamical alignment is B Scott, "Dynamical alignment in three species tokamak edge turbulence," Phys Plasmas 12 (2005) 082305.
Note: there are now auxiliary actors provided for this purpose: IMP4DV, which does the D/V conversion and enforces ambipolarity assuming absence of impurities, and IMP4imp, which subsequently enforces ambipolarity for the set of main ion and impurity species. The IMP4DV actor should be invoked directly after the transport model actor in the workflow chain, if the model produces only fluxes or if the coefficients have to be modified with the flux given. Ambipolarity is done using IMP4imp if the coreimpurity CPO is used in the workflow. These auxiliary actors are described on the auxiliary actors page.
Particle Flux as an Example
The mean field equation governing particle balance is the transport equation for electrons,
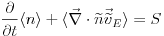
|
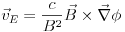
|
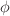 is the electrostatic potential.
is the electrostatic potential.
The angle brackets denote the flux surface average, and we will use the property that the flux surface average of a divergence of a vector is the volume derivative of the flux surface average of a contravariant volume component of the vector, in this case
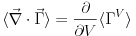
|
 is the particle flux whose flux-surface averaged volume component is
is the particle flux whose flux-surface averaged volume component is
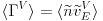
|
This is converted to expression in terms of the radial coordinate
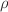 using the fact that both
using the fact that both
 and
and
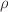 are flux quantities whose gradients are
parallel to each other. We have
are flux quantities whose gradients are
parallel to each other. We have
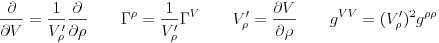
|
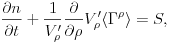
|
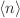 with
with
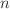 following the assumptions of the 1-D version of
mean field transport theory.
following the assumptions of the 1-D version of
mean field transport theory.
With all quantities now expressed in terms of flux quantities, we are
free to characterise the transport flux
 in an arbitrary way, so
long as only flux quantities appear. The flux expansion within
the flux surface as well as expansion or contraction of surfaces of constant
in an arbitrary way, so
long as only flux quantities appear. The flux expansion within
the flux surface as well as expansion or contraction of surfaces of constant
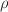 is treated using the metric coefficient
is treated using the metric coefficient
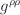 which is dimensionless.
This way we can characterise transport in terms of an effective diffusivity
and an effective frictional slip velocity which are given in SI units.
By convention both of these are done solely via
which is dimensionless.
This way we can characterise transport in terms of an effective diffusivity
and an effective frictional slip velocity which are given in SI units.
By convention both of these are done solely via
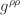 for convenience, also reflecting
that the effective velocity is actually marking off-diagonal diffusive
elements. Our convention for this follows the ETS code and is given by
for convenience, also reflecting
that the effective velocity is actually marking off-diagonal diffusive
elements. Our convention for this follows the ETS code and is given by
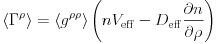
|
Metric Coefficients
Transport modellers want the Ds and Vs as physical quantities in
SI units. In general the fluxes are (magnetic) flux surface averaged
quantities, which implies the existence of metric elements in the
conversion. In our case we need
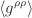 where
where 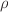 is the toroidal flux
radius in meters, so the metric elements are dimensionless. In the
equilibrium CPO, this is gm3 under
equilibrium%profiles_1d in the structure.
is the toroidal flux
radius in meters, so the metric elements are dimensionless. In the
equilibrium CPO, this is gm3 under
equilibrium%profiles_1d in the structure.
Note this is different from the ASTRA code which casts the Vs as proper
velocities, i.e., with one factor of grad-rho given by
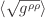 which is gm7 under
equilibrium%profiles_1d in the structure.
The units are the same and the informational content is the same, but
this difference has to be taken into account in any transport modelling
and benchmarking.
which is gm7 under
equilibrium%profiles_1d in the structure.
The units are the same and the informational content is the same, but
this difference has to be taken into account in any transport modelling
and benchmarking.
Heat Fluxes
The heat flux is treated in a similar way, with transport equation
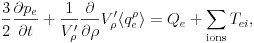
|
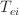 giving the species transfer
and
giving the species transfer
and 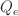 the source. For ExB transport the heat
flux has a advective (also called convective) and a conductive piece
given by
the source. For ExB transport the heat
flux has a advective (also called convective) and a conductive piece
given by
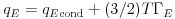
|
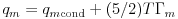
|
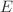 and
and
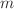 refer to the ExB eddy and magnetic flutter
channels, respectively. For reasons given below we are neglecting the
magnetic flutter piece
refer to the ExB eddy and magnetic flutter
channels, respectively. For reasons given below we are neglecting the
magnetic flutter piece
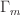 for the time being, and then the
flutter piece merely adds to the heat diffusivity.
for the time being, and then the
flutter piece merely adds to the heat diffusivity.
The forms of these due to the fluctuations are then
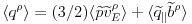
|

|
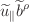 nonlinearity (in the delivery of the results, not in the turbulence
computations themselves).
nonlinearity (in the delivery of the results, not in the turbulence
computations themselves).
The total conductive flux is then represented by
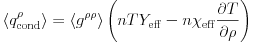
|
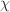 and
and 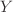 giving the heat diffusion and frictional slip pieces for each species,
respectively (these are in diff_eff and vconv_eff in the CPO for each
quantity).
giving the heat diffusion and frictional slip pieces for each species,
respectively (these are in diff_eff and vconv_eff in the CPO for each
quantity).
Operationally, the turbulence module communicates the diff_eff and vconv_eff due to each transport channel for each species to the transport solver, and the metric coefficients are used by both modules. The two modules can be on arbitrarily different grids, which communicate through standard interpolation. This despite the fact that transport at the micro-level is angle dependent (in general, it can be 3-D in the time average if the sources are 3-D). The effective transport is 1-D so long as parallel sound transit within the flux surface remains fast compared to the local transport time. This breaks down anyway in the edge, so the fact that the volume is a problematic coordinate and the flux surface average is a problematic operation on open field lines doesn't enter.
Ds and Vs from Turbulence Codes to Transport Solvers
To serve the results from turbulence codes to transport solvers, we have to turn the fluxes (results) into diffusivities and effective velocities (coefficients, Ds and Vs for short), which represent more information than is at hand. Transport solvers must work with Ds and Vs because they use implicit schemes. The matrix must be diagonally dominant; hence one cannot simply use the Vs. Fluxes which are zero and/or negative should be given with positive diffusivities for the solvers to work. We need a set of rules to provide this.
Considering the particle and heat transport fluxes for a given species, we convert the gradient in to a logarithmic derivative and express the flux in terms of a specific flux, which has units of velocity,
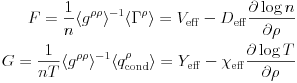
|
 )
enters.
)
enters.
The choice of what to do with the Ds and Vs is somewhat arbitrary. The needs of implicit transport solvers is for a positive D regardless of the value or sign of either flux. We decide this by putting a limit on the effective Prandtl number or its inverse: the larger specific flux is taken to be entirely diffusive, with the effective velocity set to zero. Furthermore, to address cases with very small or negative gradients, we use proxy variables for the scale lengths to calculate the provisional diffusivities before using the Prandtl number limitation to turn these into actual diffusivities. Finally, the rest of the flux is asigned to the effective velocity, so that the D and V formula reflects the actual specific flux.
The Prandtl number limitation is expressed as follows. If the smaller specific flux is within a factor of 5 of the larger, then both are purely diffusive and the effective velocities are both zero. If not, then the D ratio is set to 5, with the result that the smaller D, having been corrected, is accompanied by the corresponding V, which is now nonzero. The specific flux with the larger D will be returned with a V which is zero.
The rationale is that the turbulent mixing by the ExB velocity affects all processes, but that linear forcing can shift the average phase shift of the fluctuations such that the effective flux can be small or negative. The simplest example is adiabatic electrons, for which the ion heat flux is robust but the particle flux is zero. In most situations the specific heat flux will be the larger, and hence the familiar situation is that of a D and V for the particle flux but a D (the chi) only for the conductive heat flux.
The full algorithm starting with the specific fluxes appears as
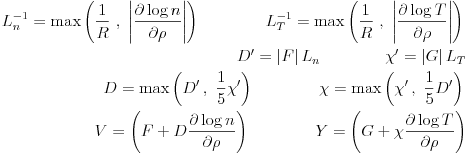
|
Note how in the end the actual gradients are used. If the gradients are moderate then their actual values are used, and if the Prandtl correction is not invoked, then both channels are diagonal. In any case the full relation is used to get the effective velocities (V and Y) so having set the rules to handle the arbitrariness of the diffusivities (D and chi) to guarantee reasonable diagonal dominance in a transport solver, the D's and V's agree with the fluxes themselves.
If there are more than two specific fluxes per species to consider, then we treat each scale length separately as above and use N-way maxima in the Prandtl correction for the N channels.
Ambipolarity
There remains the issue of ambipolarity of the D and V for particle flux. For a pure singly charged plasma the ion and electron Ds and Vs should be equal. Even if the turbulence model is gyrokinetic or gyrofluid, in which case the gyrocenter charge density is not zero but is equal to the generalised vorticity (polarisation), the quantities given to a transport solver should follow the rules for a fluid representation. However, transport modelling usually applies ambipolarity rules to the electrons after computing the ions, while the action of turbulence is actually the other way around: Dynamical alignment refers to the process by which (1) electron parallel dynamics controls the electrostatic fluctuations, then (2) the resulting ExB velocity advects all species equally. So we correct the particle fluxes by assuming the electrons determine the D according to the above procedure and then (1) the fluctuations in the flux-inducing part of the spectrum for the logarithmic densities are the same, and (2) the D's are the same. Then the V's are solved for again, by taking
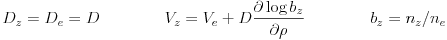
|
Statistical Character
Turbulence has a statistical character, so convergence to a mean is not monotonic and when within one std dev of the mean there is no further convergence. The diffusivity for ExB turbulence is comparable to
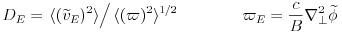
|
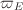 is the ExB vorticity fluctuation, and
these angle brackets denote the ensemble average. To get an ensemble
average over a statistical quantity in practice, one must do some sort
of finite-time running averaging.
is the ExB vorticity fluctuation, and
these angle brackets denote the ensemble average. To get an ensemble
average over a statistical quantity in practice, one must do some sort
of finite-time running averaging.
For transport modelling, the transport coefficients derived from a turbulence code should always be given in terms of running exponential averages.
A HOWTO for loading the coretransp CPO is given here.
last update: 2015-03-27 by bds
